Cho tứ diện ABCD có G là điểm thỏa mãn

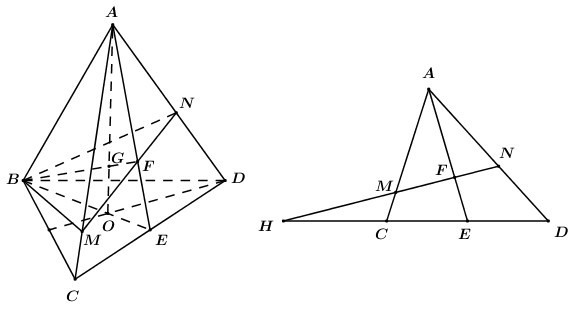
Gọi O là trọng tâm tam giác BCD

\[\begin{array}{*{20}{l}}{ \Rightarrow \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 3\overrightarrow {GO} }\\{ \Rightarrow \overrightarrow {GA} + 3\overrightarrow {GO} = \vec 0}\\{ \Rightarrow \overrightarrow {GA} = - 3\overrightarrow {GO} }\\{ \Rightarrow \frac{{AG}}{{AO}} = \frac{3}{4}}\end{array}\]

Trong (ABE) gọi\[F = BG \cap AE\,\,\left( {F \in AE} \right)\]

Lấy\[M \in AC\]  trong (ACD) gọi\[N = MF \cap AD\,\,\,\left( {N \in AD} \right)\] khi đó ta có mặt phẳng chứa BG cắt AC,AD lần lượt tại M,N chính là (BMN).

Áp dụng định lí Menelaus trong tam giác AOE, cát tuyến BGF:

\[\frac{{GA}}{{GO}}.\frac{{BO}}{{BE}}.\frac{{FE}}{{FA}} = 1 \Rightarrow 3.\frac{2}{3}.\frac{{FE}}{{FA}} = 1 \Rightarrow \frac{{FE}}{{FA}} = \frac{1}{2} \Rightarrow \frac{{AF}}{{AE}} = \frac{2}{3} \Rightarrow F\] là trọng tâm tam giác ACD.

Trong (ACD) kéo dài MN cắt CD tại H. Đặt \[\frac{{AM}}{{AC}} = x\left( {0 < x < 1} \right)\]

 Áp dụng định lí Menelaus trong tam giác ACE, cát tuyến MHF:\[\frac{{MA}}{{MC}}.\frac{{HC}}{{HE}}.\frac{{FE}}{{FA}} = 1 \Rightarrow \frac{x}{{1 - x}}.\frac{{HC}}{{HE}}.\frac{1}{2} = 1 \Rightarrow \frac{{HC}}{{HE}} = \frac{{2\left( {1 - x} \right)}}{x}\]

\[\begin{array}{*{20}{l}}{ \Rightarrow HE = \frac{x}{{2\left( {1 - x} \right)}}HC}\\{ \Rightarrow HC + CE = \frac{x}{{2\left( {1 - x} \right)}}HC}\\{ \Rightarrow CE = \frac{{3x - 2}}{{2\left( {1 - x} \right)}}HC}\end{array}\]

Ta có:

\[\begin{array}{*{20}{l}}{HD = HC + 2CE}\\{\,\,\,\,\,\,\,\,\, = HC + \frac{{3x - 2}}{{1 - x}}HC = \frac{{2x - 1}}{{1 - x}}HC}\\{ \Rightarrow \frac{{HE}}{{HD}} = \frac{x}{{2\left( {1 - x} \right)}}:\frac{{2x - 1}}{{1 - x}} = \frac{x}{{2\left( {2x - 1} \right)}}}\end{array}\]

Áp dụng định lí Menelaus trong tam giác AED, cát tuyến MFN:

\[\begin{array}{*{20}{l}}{\frac{{FA}}{{FE}}.\frac{{HE}}{{HD}}.\frac{{ND}}{{NA}} = 1 \Rightarrow 2.\frac{x}{{2\left( {2x - 1} \right)}}.\frac{{ND}}{{NA}} = 1}\\{ \Rightarrow \frac{{ND}}{{NA}} = \frac{{2x - 1}}{x} \Rightarrow \frac{{NA}}{{ND}} = \frac{x}{{2x - 1}}}\\{ \Rightarrow \frac{{NA}}{{NA + ND}} = \frac{x}{{x + 2x - 1}} = \frac{x}{{3x - 1}}}\\{ \Rightarrow \frac{{AN}}{{AD}} = \frac{x}{{3x - 1}}}\end{array}\]

Khi đó ta có\[\frac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \frac{{AM}}{{AC}}.\frac{{AN}}{{AD}} = x.\frac{x}{{3x - 1}} = \frac{{{x^2}}}{{3x - 1}}\,\,\left( {x > \frac{1}{3}} \right)\]

Xét hàm số \[f\left( x \right) = \frac{{{x^2}}}{{3x - 1}}\,\,\left( {x > \frac{1}{3}} \right)\]  ta có

\[f'\left( x \right) = \frac{{2x\left( {3x - 1} \right) - 3{x^2}}}{{{{\left( {3x - 1} \right)}^2}}} = \frac{{3{x^2} - 2x}}{{{{\left( {3x - 1} \right)}^2}}};f\prime (x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0\,(ktm)}\\{x = \frac{2}{3}}\end{array}} \right.\]

BBT:

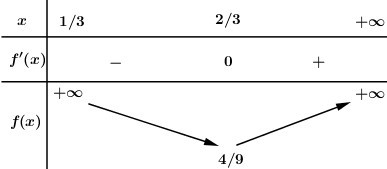
Dựa vào BBT ta thấy\[\mathop {\min }\limits_{\left( {\frac{1}{3}; + \infty } \right)} f\left( x \right) = f\left( {\frac{2}{3}} \right) = \frac{4}{9}\]

Vậy giá trị nhỏ nhất của tỉ số\[\frac{{{V_{ABMN}}}}{{{V_{ABCD}}}} = \frac{4}{9}\]