Trong không gian với hệ tọa độ Oxyz, cho đường thẳng

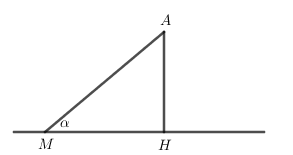
Đường thẳng \[\Delta \] đi qua điểm\[M\left( {2;5;7 - 2\sqrt 2 } \right)\] và nhận\[\vec u = \left( {{m^2} - 2m;4 - m;0} \right)\] làm VTCP.

Có\[\overrightarrow {AM} = \left( {1;3;4 - 2\sqrt 2 } \right) \Rightarrow AM = \sqrt {34 - 16\sqrt 2 } \]

Để\[d\left( {A,{\rm{\Delta }}} \right) = A{H_{\min }}\]  thì\[\sin \alpha = \frac{{AH}}{{AM}}\] đạt GTNN hay cosα đạt GTLN.

Mà

\[\cos \alpha = \cos \left( {AM,{\rm{\Delta }}} \right) = \frac{{\left| {\overrightarrow {AM} .\vec u} \right|}}{{\left| {\overrightarrow {AM} } \right|.\left| {\vec u} \right|}} = \frac{{\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right|}}{{\sqrt {34 - 16\sqrt 2 } .\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} }}\]

Mà

\[\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right| \le \sqrt {{1^2} + {3^2}} .\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} \]

\[ \Rightarrow \frac{{\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right|}}{{\sqrt {34 - 16\sqrt 2 } .\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} }} \le \frac{{\sqrt {10} }}{{\sqrt {34 - 16\sqrt 2 } }}\]

\[ \Rightarrow \cos \alpha \] đạt GTLN nếu

\[\frac{{{m^2} - 2m}}{1} = \frac{{4 - m}}{3} \Leftrightarrow 3{m^2} - 6m = 4 - m \Leftrightarrow 3{m^2} - 5m - 4 = 0\]

Phương trình này có hai nghiệm phân biệt do ac<0 nên tổng các giá trị của m là \(\frac{5}{3}\) .