Cho hình nón có góc ở đỉnh bằng 120 độ và đường cao bằng 2.
Câu hỏi :
Cho hình nón có góc ở đỉnh bằng \({120^0}\) và đường cao bằng 2. Tính diện tích xung quanh của hình nón đã cho.
Cho hình nón có góc ở đỉnh bằng \({120^0}\) và đường cao bằng 2. Tính diện tích xung quanh của hình nón đã cho.
D. \(8\pi \)
* Đáp án
B
* Hướng dẫn giải
Đáp án B
Phương pháp giải:
- Sử dụng tính chất tam giác cân: Đường trung tuyến đồng thời là đường phân giác.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính độ dài đường sinh \(l\) và bán kính đáy \(r\) của hình nón.
- Áp dụng công thức tính diện tích xung quanh của hình nón có độ dài đường sinh \(l\) và bán kính đáy \(r\) là \({S_{xq}} = \pi rl\).
Giải chi tiết:
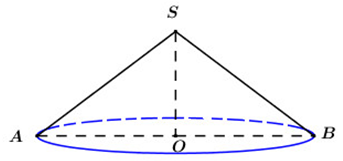
Gọi \(S\) là đỉnh hình nón, \(AB\) là 1 đường kính của hình nón và \(O\) là tâm đường tròn đáy của hình nón.
Khi đó ta có \(\angle ASB = {120^0}\) và \(h = SO = 2\).
Ta có: \(\Delta SAB\) cân tại \(S\) suy ra \(SO\) là phân giác của \(\angle ASB\).
\( \Rightarrow \angle ASO = \frac{1}{2}\angle ASB = {60^0}\)
Xét tam giác vuông \(SOA\) có: \(r = OA = SO.\tan {60^0} = 2\sqrt 3 \), \(l = SA = \frac{{SO}}{{\cos {{60}^0}}} = 4\)
Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi .2\sqrt 3 .4 = 8\sqrt 3 \pi \).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án !!
Copyright © 2021 HOCTAP247
