Một que kem ốc quế gồm hai phần : phần kem có dạng hình cầu
Câu hỏi :
Một que kem ốc quế gồm hai phần : phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón cùng có bán kính bằng \(3{\mkern 1mu} cm,\) chiều cao hình nón là \(9cm.\) Thể tích của que kem (bao gồm cả phần không gian bên trong ốc quế không chứa kem) có giá trị bằng:
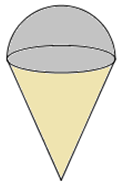
Một que kem ốc quế gồm hai phần : phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón cùng có bán kính bằng \(3{\mkern 1mu} cm,\) chiều cao hình nón là \(9cm.\) Thể tích của que kem (bao gồm cả phần không gian bên trong ốc quế không chứa kem) có giá trị bằng:

D. \(45\left( {c{m^3}} \right).\)
* Đáp án
A
* Hướng dẫn giải
Đáp án A
Phương pháp giải:
Công thức tính thể tích của khối nón có bán kính đáy R và chiều cao h là: \(V = \frac{1}{3}\pi {R^2}h.\)
Công thức tính thể của khối cầu có bán kính R là: \(V = \frac{4}{3}\pi {R^3}.\)
Giải chi tiết:
Ta có thể tích của phần kem là: \({V_1} = \frac{1}{2}.\frac{4}{3}.\pi {R^3}\)\( = \frac{2}{3}\pi {.3^3} = 18\pi {\mkern 1mu} {\mkern 1mu} c{m^3}.\)
Thể tích của phần ốc quế bên dưới là: \({V_2} = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {.3^2}.9 = 27\pi {\mkern 1mu} {\mkern 1mu} c{m^3}.\)
Vậy \(V = {V_1} + {V_2} = 18\pi + 27\pi = 45\pi {\mkern 1mu} {\mkern 1mu} c{m^3}.\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án !!
Copyright © 2021 HOCTAP247
