Cho tứ diện ABCD có AC = a, BD = 3a. Gọi M và N lần lượt là trung điểm

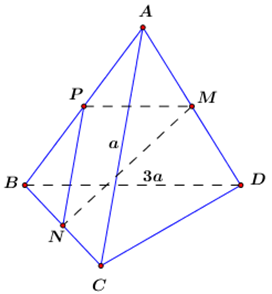
Gọi \[P\] là trung điểm của \[AB\].

Ta có: \[PM,{\mkern 1mu} {\mkern 1mu} PN\] lần lượt là đường trung bình của \[\Delta ACD,{\mkern 1mu} {\mkern 1mu} \Delta ABC\] nên \[PM = \frac{1}{2}BD = \frac{{3a}}{2}\], \[PN = \frac{1}{2}AC = \frac{a}{2}\] và \[\left\{ {\begin{array}{*{20}{l}}{PM\parallel BD}\\{PN\parallel AC}\end{array}} \right.\].

Mà \[AC \bot BD{\mkern 1mu} {\mkern 1mu} \left( {gt} \right)\] nên \[PM \bot PN\], do đó tam giác \[PMN\] vuông tại \[P\].

Áp dụng định lí Pytago ta có: \[MN = \sqrt {P{M^2} + P{N^2}} \]\[ = \sqrt {\frac{{9{a^2}}}{4} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt {10} }}{2}\].