Trong không gian cho hai điểm A,B cố định và độ dài đoạn thẳng AB bằng 4
Câu hỏi :
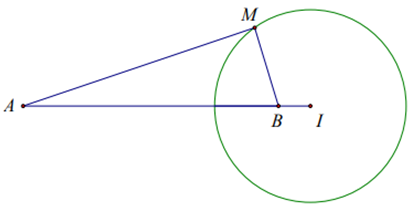
Trong không gian cho hai điểm \[A,B\] cố định và độ dài đoạn thẳng \[AB\] bằng 4. Biết rằng tập hợp các điểm \[M\] sao cho \[MA = 3MB\] là một mặt cầu. Tìm bán kính \[R\] của mặt cầu đó?
Trong không gian cho hai điểm \[A,B\] cố định và độ dài đoạn thẳng \[AB\] bằng 4. Biết rằng tập hợp các điểm \[M\] sao cho \[MA = 3MB\] là một mặt cầu. Tìm bán kính \[R\] của mặt cầu đó?
D. \(R = 1.\)
* Đáp án
C
* Hướng dẫn giải
Đáp án C
Giải chi tiết:
Gọi \(I\) là điểm thỏa mãn \(\overrightarrow {IA} = 9\overrightarrow {IB} \)
\(MA = 3MB \Leftrightarrow M{A^2} = 9M{B^2}\)
\( \Leftrightarrow {\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} = 9{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2}\)
\( \Leftrightarrow {\overrightarrow {MI} ^2} + 2\overrightarrow {MI} .\overrightarrow {IA} + {\overrightarrow {IA} ^2} = 9{\overrightarrow {MI} ^2} + 18\overrightarrow {MI} .\overrightarrow {IB} + 9{\overrightarrow {IB} ^2}\)
\( \Leftrightarrow - 8M{I^2} + 2\overrightarrow {MI} \left( {\overrightarrow {IA} - 9\overrightarrow {IB} } \right) = 9I{B^2} - I{A^2}\)
\( \Leftrightarrow M{I^2} = \frac{{I{A^2} - 9I{B^2}}}{8}\)
Dễ dàng tính được \(IA = \frac{9}{8}AB = \frac{9}{2}{\mkern 1mu} ;{\mkern 1mu} {\mkern 1mu} IB = \frac{1}{8}AB = \frac{1}{2}\)
\( \Rightarrow R = MI = \sqrt {\frac{{I{A^2} - 9I{B^2}}}{8}} = \sqrt {\frac{{{{\left( {\frac{9}{2}} \right)}^2} - {{\left( {\frac{1}{2}} \right)}^2}}}{8}} = \frac{3}{2}\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án !!
Copyright © 2021 HOCTAP247
