Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Số nghiệm của
Câu hỏi :
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.
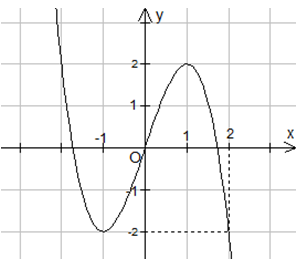
Số nghiệm của phương trình \(f\left( {f\left( x \right)} \right) = - 2\) là
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ.

Số nghiệm của phương trình \(f\left( {f\left( x \right)} \right) = - 2\) là
* Đáp án
* Hướng dẫn giải
Đáp án: 5
Phương pháp giải:
- Đặt \(t = f\left( x \right)\), dựa vào tương giao đồ thị giải phương trình tìm t.
- Tiếp tục sử dụng tương giao tìm số nghiệm x.
Giải chi tiết:
Đặt \(t = f\left( x \right)\), phương trình trở thành \(f\left( t \right) = - 2\).
Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(y = - 2\).
Dựa vào đồ thị hàm số ta thấy: Phương trình có nghiệm \(\left[ {\begin{array}{*{20}{l}}{t = - 2}\\{t = 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{f\left( x \right) = - 2}\\{f\left( x \right) = 1}\end{array}} \right.\).
Tiếp tục dựa vào đồ thị hàm số ta thấy:
Phương trình \(f\left( x \right) = - 2\) có 2 nghiệm phân biệt.
Phương trình \(f\left( x \right) = 1\) có 3 nghiệm phân biệt.
Vậy phương trình ban đầu có tất cả 5 nghiệm phân biệt.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án !!
Copyright © 2021 HOCTAP247
