Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau
Câu hỏi :
Cho tứ diện \(OABC\) có ba cạnh \(OA,{\mkern 1mu} {\mkern 1mu} OB,{\mkern 1mu} {\mkern 1mu} OC\) đôi một vuông góc với nhau. Biết khoảng cách từ điểm \(O\) đến các đường thẳng \(BC,{\mkern 1mu} {\mkern 1mu} CA,{\mkern 1mu} {\mkern 1mu} AB\) lần lượt là \(a,{\mkern 1mu} {\mkern 1mu} a\sqrt 2 ,{\mkern 1mu} {\mkern 1mu} a\sqrt 3 \). Tính khoảng cách từ điểm \(O\) đến mặt phẳng \(\left( {ABC} \right)\) theo a.
Cho tứ diện \(OABC\) có ba cạnh \(OA,{\mkern 1mu} {\mkern 1mu} OB,{\mkern 1mu} {\mkern 1mu} OC\) đôi một vuông góc với nhau. Biết khoảng cách từ điểm \(O\) đến các đường thẳng \(BC,{\mkern 1mu} {\mkern 1mu} CA,{\mkern 1mu} {\mkern 1mu} AB\) lần lượt là \(a,{\mkern 1mu} {\mkern 1mu} a\sqrt 2 ,{\mkern 1mu} {\mkern 1mu} a\sqrt 3 \). Tính khoảng cách từ điểm \(O\) đến mặt phẳng \(\left( {ABC} \right)\) theo a.
* Đáp án
* Hướng dẫn giải
Đáp án: \(\frac{{2a\sqrt {33} }}{{11}}\)
Phương pháp giải:
- Kẻ \(OM \bot AC{\mkern 1mu} {\mkern 1mu} \left( {M \in AC} \right)\), \(ON \bot AB{\mkern 1mu} {\mkern 1mu} \left( {N \in AB} \right)\), \(OP \bot BC{\mkern 1mu} {\mkern 1mu} \left( {P \in BC} \right)\). Khi đó ta có \(OP = a,\) \(OM = a\sqrt 2 ,\) \(ON = a\sqrt 3 \).
- Trong \[\left( {OCN} \right)\] kẻ \[OH \bot CN{\mkern 1mu} {\mkern 1mu} \left( {H \in CN} \right)\], chứng minh \[OH \bot \left( {ABC} \right)\].
- Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Giải chi tiết:
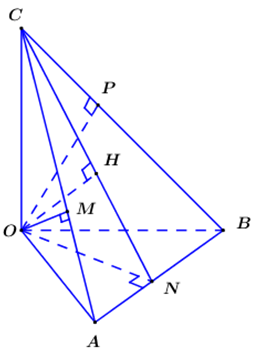
Kẻ \(OM \bot AC{\mkern 1mu} {\mkern 1mu} \left( {M \in AC} \right)\), \(ON \bot AB{\mkern 1mu} {\mkern 1mu} \left( {N \in AB} \right)\), \(OP \bot BC{\mkern 1mu} {\mkern 1mu} \left( {P \in BC} \right)\)
Khi đó ta có \[OP = a,{\mkern 1mu} {\mkern 1mu} OM = a\sqrt 2 ,{\mkern 1mu} {\mkern 1mu} ON = a\sqrt 3 \]
Trong \(\left( {OCN} \right)\) kẻ \(OH \bot CN{\mkern 1mu} {\mkern 1mu} \left( {H \in CN} \right)\) ta có:
\(\left\{ {\begin{array}{*{20}{l}}{AB \bot ON}\\{AB \bot OC}\end{array}} \right. \Rightarrow AB \bot \left( {OCN} \right) \Rightarrow AB \bot OH\)
\(\left\{ {\begin{array}{*{20}{l}}{OH \bot AB}\\{OH \bot CN}\end{array}} \right. \Rightarrow OH \bot \left( {ABC} \right) \Rightarrow d\left( {O;\left( {ABC} \right)} \right) = OH\)
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{C^2}}} + \frac{1}{{O{N^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Lại có: \(\frac{1}{{O{M^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{C^2}}};{\mkern 1mu} {\mkern 1mu} \frac{1}{{O{N^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}};{\mkern 1mu} {\mkern 1mu} \frac{1}{{O{P^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
\( \Rightarrow \frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} + \frac{1}{{O{P^2}}} = 2\left( {\frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}} \right)\)
\( \Rightarrow \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{2}\left( {\frac{1}{{O{M^2}}} + \frac{1}{{O{N^2}}} + \frac{1}{{O{P^2}}}} \right)\)
\( \Rightarrow \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}} = \frac{1}{2}\left( {\frac{1}{{2{a^2}}} + \frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}}} \right) = \frac{{11}}{{12{a^2}}}\)
\( \Rightarrow \frac{1}{{O{H^2}}} = \frac{{11}}{{12{a^2}}} \Rightarrow OH = \frac{{2a\sqrt {33} }}{{11}}\)
Vậy \(d\left( {O;\left( {ABC} \right)} \right) = \frac{{2a\sqrt {33} }}{{11}}\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án !!
Copyright © 2021 HOCTAP247
