Cắt hình nón bởi một mặt phẳng qua trục thu được thiết diện là một tam giác

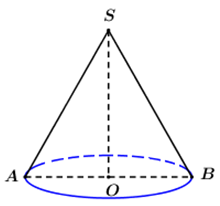
Giả sử thiết diện qua trục là tam giác \(SAB\), \(O\) là tâm đường tròn đáy \( \Rightarrow O\) là trung điểm của \(AB\)

Tam giác \(SAB\) vuông tại \(S\) nên \({S_{\Delta SAB}} = \frac{1}{2}SA.SB = \frac{1}{2}S{A^2} = 8 \Leftrightarrow SA = 4 = l\)

\( \Rightarrow AB = SA\sqrt 2 = 4\sqrt 2 \Rightarrow r = OA = 2\sqrt 2 \).

Vậy diện tích xung quanh hình nón là \({S_{xq}} = \pi rl = \pi .2\sqrt 2 .4 = 8\sqrt 2 \pi \)