Cho hình nón có chiều cao h = 10 và bán kính đáy r = 5. Xét hình trụ

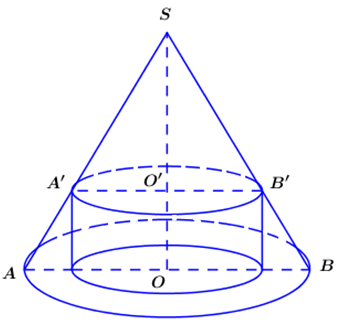
Theo bài ra ta có \(SO = 10,{\mkern 1mu} {\mkern 1mu} OA = 5\)

Đặt \(O'A' = r{\rm{ }}\left( {0 < r < 5} \right)\)

Áp dụng định lí Ta-lét ta có \(\frac{{O'A'}}{{OA}} = \frac{{SO'}}{{SO}} \Rightarrow \frac{r}{5} = \frac{{SO'}}{{10}} \Leftrightarrow SO' = 2r \Rightarrow OO' = 10 - 2r\)

Khi đó thể tích khối trụ là: \(V = \pi .O'{A'^2}.OO' = \pi .{r^2}\left( {10 - 2r} \right) = 2\pi \left( { - {r^3} + 5{r^2}} \right)\).

Xét hàm số \(f\left( r \right) = - {r^3} + 5{r^2}\) trên \(\left( {0;5} \right)\) ta có \(f'\left( r \right) = - 3{r^2} + 10r = 0 \Leftrightarrow \left[ \begin{array}{l}r = 0{\rm{ }}\left( {ktm} \right)\\r = \frac{{10}}{3}\end{array} \right.\).

Vậy để thể tích khối trụ đạt GTLN thì bán kính khối trụ bằng \(\frac{{10}}{3}\).