Cho hàm số y = f(x) xác định và liên tục trên R, có đồ thị như hình vẽ.
Câu hỏi :
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ. Hàm số \(g\left( x \right) = f\left( {{x^2} - 2} \right)\) có bao nhiêu điểm cực tiểu?
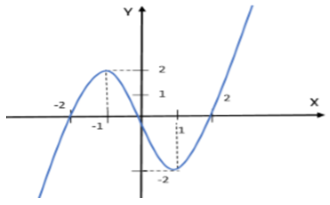
Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\), có đồ thị như hình vẽ. Hàm số \(g\left( x \right) = f\left( {{x^2} - 2} \right)\) có bao nhiêu điểm cực tiểu?

A. 3
B. 1
C. 5
D. 2
* Đáp án
A
* Hướng dẫn giải
Đáp án A
Phương pháp giải:
- Tính đạo hàm hàm số \(y = g\left( x \right)\)
- Giải phương trình \(g'\left( x \right) = 0\)
- Lập bảng xét dấu \(g'\left( x \right)\)
- Xác định các điểm cực tiểu của hàm số \(g\left( x \right)\) là các điểm mà qua đó \(g'\left( x \right)\) đổi dấu từ âm sang dương.
Giải chi tiết:
Dựa vào đồ thị hàm số ta thấy: Hàm số có 2 điểm cực trị \(x = - 1,{\mkern 1mu} {\mkern 1mu} x = 1\), do đó \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = - 1}\end{array}} \right.\)
Ta có \(g'\left( x \right) = 2x.f'\left( {{x^2} - 2} \right)\)
\(g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{f'\left( {{x^2} - 2} \right) = 0}\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{{x^2} - 2 = 1}\\{{x^2} - 2 = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = \pm \sqrt 3 }\\{x = \pm 1}\end{array}} \right.\)
Ta có bảng xét dấu \(g'\left( x \right)\) như sau:

Dựa vào bảng xét dấu ta thấy, \(g'\left( x \right)\) đổi dấu từ âm sang dương khi đi qua các điểm \(x = - \sqrt 3 \), \(x = 0\), \(x = \sqrt 3 \)
Vậy hàm số \(y = g\left( x \right)\) có 3 điểm cực tiểu.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án !!
Copyright © 2021 HOCTAP247
