Cho khối tứ diện ABCD. Gọi M,N,E lần lượt là trung điểm của

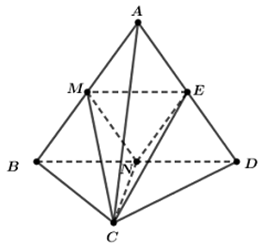
Ta có: \({V_{ABCD}} = {V_{C.ABD}} = \frac{1}{3}{S_{ABD}}.d\left( {C,\left( {ABD} \right)} \right)\)

\({V_{MNEC}} = {V_{C.MNE}} = \frac{1}{3}{S_{MNE}}.d\left( {C,\left( {MNE} \right)} \right) = \frac{1}{3}{S_{MNE}}.d\left( {C,\left( {ABD} \right)} \right)\)

\( \Rightarrow \frac{{{V_{MNEC}}}}{{{V_{ABCD}}}} = \frac{{\frac{1}{3}{S_{MNE}}.d\left( {C,\left( {ABD} \right)} \right)}}{{\frac{1}{3}{S_{ABD}}.d\left( {C,\left( {ABD} \right)} \right)}} = \frac{{{S_{MNE}}}}{{{S_{ABD}}}}\)

Dễ thấy \(\Delta MNE\) đồng dạng \(\Delta DAB\) theo tỉ số \(\frac{1}{2}\) nên \(\frac{{{S_{MNE}}}}{{{S_{ABD}}}} = {\left( {\frac{1}{2}} \right)^2} = \frac{1}{4}\)

Vậy \(\frac{{{V_{MNEC}}}}{{{V_{ABCD}}}} = \frac{{{S_{MNE}}}}{{{S_{ABD}}}} = \frac{1}{4}\).