Ký hiệu M và m tương ứng là GTLN và GTNN của hàm số y = x^2 - 2x + 5
Câu hỏi :
Ký hiệu \[M\] và \[m\] tương ứng là GTLN và GTNN của hàm số \(y = {x^2} - 2x + 5\) trên miền \(\left[ {2;7} \right].\) Phát biểu nào sau đây đúng?
Ký hiệu \[M\] và \[m\] tương ứng là GTLN và GTNN của hàm số \(y = {x^2} - 2x + 5\) trên miền \(\left[ {2;7} \right].\) Phát biểu nào sau đây đúng?
* Đáp án
* Hướng dẫn giải
Đáp án: \(8m\)
Phương pháp giải:
Xác định hoành độ đỉnh \({x_I}\) xem có thuộc đoạn \(\left[ {a;b} \right]\) cần tìm GTLN, GTNN hay không?
Nếu \({x_I} \notin \left[ {a;b} \right]\) thì ta tính \(f\left( a \right);f\left( b \right)\)và so sánh ta được GTLN, GTNN.
Giải chi tiết:
Xét hàm số \(y = {x^2} - 2x + 5\) trên \(\left[ {2;{\mkern 1mu} {\mkern 1mu} 7} \right]\) ta có BBT:
Đỉnh của đồ thị hàm số \(y = {x^2} - 2x + 5\) là \(I\left( {1;{\mkern 1mu} {\mkern 1mu} 4} \right)\)
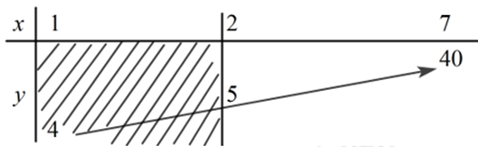
Dựa vào BBT ta có: \(M = \mathop {Max}\limits_{\left[ {2;{\kern 1pt} {\kern 1pt} 7} \right]} y = 40\) khi \(x = 7\) và \(m = \mathop {Min}\limits_{\left[ {2;{\kern 1pt} {\kern 1pt} 7} \right]} y = 5\) khi \(x = 2\).
\( \Rightarrow M = 8m\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Top 5 đề thi Đánh giá năng lực trường ĐHQG Hà Nội có đáp án !!
Copyright © 2021 HOCTAP247
