Cho lăng trụ đều ABC.A'B'C' có tất cả các cạnh bằng a.

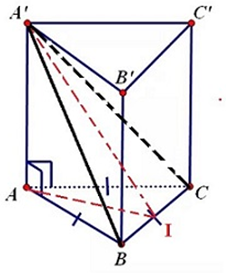
Gọi \(I\) là trung điểm của \(BC\).

Vì \(\Delta ABC\) đều nên \(AI \bot BC\) và \(AI = \frac{{a\sqrt 3 }}{2}\)

\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{BC \bot AI}\\{BC \bot AA'}\end{array}} \right. \Rightarrow BC \bot \left( {AIA'} \right) \Rightarrow BC \bot A'I\)

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {ABC} \right) \cap \left( {A'BC} \right) = BC}\\{AI \subset \left( {ABC} \right),{\mkern 1mu} AI \bot BC}\\{A'I \subset \left( {ABC} \right),{\mkern 1mu} A'I \bot BC}\end{array}} \right. \Rightarrow \alpha = \angle \left( {\left( {ABC} \right);\left( {A'BC} \right)} \right) = \angle AIA'\)

Xét tam giác vuông \(AIA'\) ta có: \(\tan \alpha = \frac{{AA'}}{{AI}} = \frac{a}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{2\sqrt 3 }}{3}\).