Hai con lắc đơn giống hệt nhau mà các vật nhỏ mang điện tích như nhau,

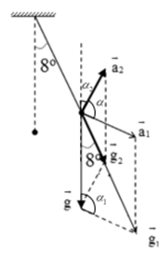
Áp dụng định lí hàm sin cho các tam giác, ta có: \[\left\{ {\begin{array}{*{20}{l}}{\frac{{{a_1}}}{{\sin {8^0}}} = \frac{g}{{\sin \left( {{{172}^0} - {\alpha _1}} \right)}} = \frac{{{g_1}}}{{\sin {\alpha _1}}}}\\{\frac{{{a_2}}}{{\sin {8^0}}} = \frac{g}{{\sin \left( {{{172}^0} - {\alpha _2}} \right)}} = \frac{{{g_2}}}{{\sin {\alpha _2}}}}\end{array}} \right.\]

Lại có: \[{a_1} = {a_2} \Rightarrow \frac{{{a_1}}}{{\sin {8^0}}} = \frac{{{a_2}}}{{\sin {8^0}}}\]

\[\frac{g}{{\sin \left( {{{172}^0} - {\alpha _1}} \right)}} = \frac{g}{{\sin \left( {{{172}^0} - {\alpha _2}} \right)}}\]

\[ \Rightarrow \sin \left( {{{172}^0} - {\alpha _1}} \right) = \sin \left( {{{172}^0} - {\alpha _2}} \right)\]

\[ \Rightarrow {172^0} - {\alpha _1} = {180^0} - \left( {{{172}^0} - {\alpha _2}} \right)\]

\[ \Rightarrow {\alpha _1} + {\alpha _2} = {164^0}\]

Xét chu kì của con lắc:

\[{T_1} = {T_2} \Rightarrow 2\pi \sqrt {\frac{l}{{{g_1}}}} = 2\pi \sqrt {\frac{l}{{{g_2}}}} \Rightarrow {g_1} = {g_2}\]

Mặt khác: \[\frac{{{g_1}}}{{\sin {\alpha _1}}} = \frac{{{g_2}}}{{\sin {\alpha _2}}} \Rightarrow \sin {\alpha _1} = \sin {\alpha _2} \Rightarrow {\alpha _1} + {\alpha _2} = {180^0}\]

→ với mọi giá trị \({\alpha _1},{\mkern 1mu} {\mkern 1mu} {\alpha _2}\) thỏa mãn \({\alpha _1} + {\alpha _2}{\mkern 1mu} = {164^0}\), luôn có \({T_2} > {T_1}\)

Góc hợp bởi hai vecto cường độ điện trường:

\(\alpha = {\alpha _1} - {\alpha _2} \Rightarrow {\alpha _1} = \alpha + {\alpha _2}\)

\( \Rightarrow \alpha + 2{\alpha _2} = {164^0} \Rightarrow {\alpha _2} = \frac{{{{164}^0} - \alpha }}{2}\)

Ta có: \({\alpha _2} \ge {0^0} \Rightarrow \frac{{{{164}^0} - \alpha }}{2} \ge {0^0} \Rightarrow \alpha \le {164^0}\)

Vậy \(\alpha \) không thể nhận giá trị \({170^0}\).