Trang chủ
Đề thi & kiểm tra
Lớp 12
Toán học
Đề thi giữa HK1 môn Toán 12 năm 2020 trường THPT Chu Văn An
Với giá trị nào của m thì phương trình \({x^4}...
Với giá trị nào của m thì phương trình \({x^4} - 3{x^2} + m = 0\) có ba nghiệm phân biệt?
Câu hỏi :
Đồ thị sau đây là của hàm số \(y = {x^4} - 3{x^2} - 3\). Với giá trị nào của m thì phương trình \({x^4} - 3{x^2} + m = 0\) có ba nghiệm phân biệt?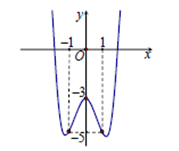
A. m = -3
B. m = -4
C. m = 0
D. m = 4
* Đáp án
C
* Hướng dẫn giải
TXĐ: \(D = \mathbb{R}\)
\({x^4} - 3{x^2} + m\)
\({x^4} - 3{x^2} + m = 0\)
\(\Leftrightarrow {x^4} - 3{x^2} = - m\)
\(\Leftrightarrow {x^4} - 3{x^2} - 3 = - m - 3\)
Số nghiệm của pt \({x^4} - 3{x^2} + m = 0\) chính là số giao điểm của đths \({x^4} - 3{x^2} - 3 = 0\) và đường thẳng \(y= -m - 3\)
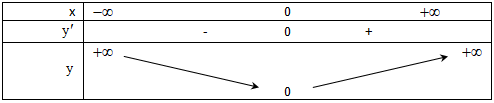
Từ đồ thị hàm số \(\Rightarrow - m – 3 = 0 \Leftrightarrow m=0\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi giữa HK1 môn Toán 12 năm 2020 trường THPT Chu Văn An
Số câu hỏi: 25
Copyright © 2021 HOCTAP247
