Cho x1=A1cos(wt+pi/3) và x2=A2cos(wt-pi/4) là hai phương trình

* Hướng dẫn giải

Đáp án B

Phương pháp: Sử dụng giản đồ vecto và định lí hàm số sin trong tam giác

Cách giải:

- Phương trình dao động của $x; x_1; x_2$: $\left\{\begin{array}{l}x=5\cos \left(\omega t+\phi \right)\\ x_1=A_1\cos \left(\omega t+\frac{\pi }{3}\right)\\ x_2=A_2\cos \left(\omega t-\frac{\pi }{4}\right)\end{array}\right.$

Suy ra:

+ Độ lệch pha giữa $x$ và $x_1$ là $\frac{\pi }{3}-\phi$

+ Độ lệch pha giữa $x$ và $x_2$ là $\phi +\frac{\pi }{4}$

+ Độ lệch pha giữa $x_1$ và $x_2$ là $\frac{\pi }{3}-\left(-\frac{\pi }{4}\right)=\frac{7\pi }{12}$

Ta có giản đồ vecto:

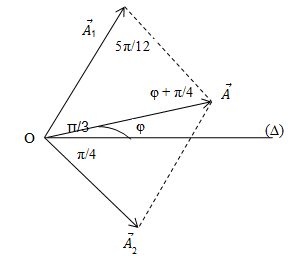
- Áp dụng định lí hàm số sin trong tam giác ta có:

$\frac{A}{\sin \frac{5\pi }{12}}=\frac{A_1}{\sin (\phi +\frac{\pi }{4})}=\frac{A_2}{\sin (\frac{\pi }{3}-\phi )}\to \left\{\begin{array}{l}{A}_1=\frac{A\sin \left(\phi +\frac{\pi }{4}\right)}{\sin \frac{5\pi }{12}}\\ A_2=\frac{A\sin \left(\frac{\pi }{3}-\phi \right)}{\sin \frac{5\pi }{12}}\end{array}\right.$

$\to A_1+A_2=\frac{A\sin \left(\phi +\frac{\pi }{4}\right)}{\sin \frac{5\pi }{12}}+\frac{A\sin \left(\frac{\pi }{3}-\phi \right)}{\sin \frac{5\pi }{12}}=\frac{A}{\sin \frac{5\pi }{12}}\left[\sin \left(\phi +\frac{\pi }{4}\right)+\sin \left(\frac{\pi }{3}-\phi \right)\right]$

- Có: $sina+sinb=2\sin \frac{a+b}{2}.c\text{os}\frac{a-b}{2}\Rightarrow \sin \left(\phi +\frac{\pi }{4}\right)+\sin \left(\frac{\pi }{3}-\phi \right)=2\sin \frac{7\pi }{24}c\text{os}\left(\phi -\frac{\pi }{24}\right)$

$\Rightarrow A_1+A_2=2A\frac{\sin \frac{7\pi }{24}}{\sin \frac{5\pi }{12}}.c\text{os}\left(\phi -\frac{\pi }{24}\right)$

Để $[A_1 + A_2]$ đạt cực đại thì: ${\left[cos\left(\phi -\frac{\pi }{24}\right)\right]}_{\text{max}}=1\Rightarrow \phi -\frac{\pi }{24}=k2\pi \Rightarrow \phi =\frac{\pi }{24}$