cho tứ diện OABC có OA,OB,OC đôi một vuông góc với nhau; OA=a;OB=2a.Thể tích khối tứ diện OABC bằng

* Hướng dẫn giải

Đáp án A

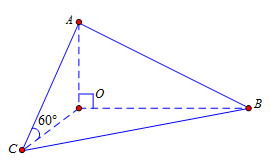
Theo giả thiết OA, OB, OC đôi một vuông góc với nhau nên $OA\perp \left(OBC\right),OC$ là hình chiếu của AC lên mặt phẳng $\left(OBC\right).$ Do đó, $\widehat{ACO}=60°,OA$ là chiều cao của tứ diện OABC. Xét tam giác vuông AOC có $\tan 60°=\frac{OA}{OC}$ với $OA=a\Rightarrow OC=\frac{OA}{\tan 60°}=\frac{a}{\sqrt{3}}=\frac{a\sqrt{3}}{3};OB=2a$ 

Ta có  $S_{OBC}=\frac{1}{2}OB.OC=\frac{1}{2}2a.\frac{a\sqrt{3}}{3};V_{OABC}=\frac{1}{3}OA.S_{OBC}=\frac{1}{3}a.\frac{a^2\sqrt{3}}{3}=\frac{a^3\sqrt{3}}{9}$