cho hình chóp SABC. Bên trong tam giác ABC ta lấy một điểm O bất kỳ.

* Hướng dẫn giải

Đáp án C

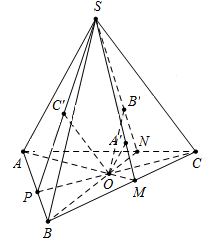
Gọi M,N,P lần lượt là giao điểm của OA, OB, OC với cạnh BC, CA, AB.

 Vì $OB\text{'}//SA\Rightarrow \frac{OA\text{'}}{SA}=\frac{OM}{AM}$ (Định lí Thalet).

Tương tự, ta có $\frac{OB\text{'}}{SB}=\frac{ON}{BN\text{'}};\frac{OC\text{'}}{SC}=\frac{OP}{PC}\Rightarrow T=\frac{OM}{AM}+\frac{ON}{BN}+\frac{OP}{PC}.$ 

Với O là trọng tâm của tam giác ABC $\Rightarrow M,N,P$ lần lượt là trung điểm của BC, CA, AB

$\Rightarrow \frac{OM}{AM}=\frac{ON}{BN}=\frac{OP}{CP}=\frac{1}{3}.$ Vậy tổng tỉ số $T=\frac{OA\text{'}}{SA}+\frac{OB\text{'}}{SB}+\frac{OC\text{'}}{SC}=1.$ 

Chú ý: Bản chất bài toán là yêu cầu chứng minh $\frac{OM}{AM}+\frac{ON}{BN}+\frac{OP}{PC}=1.$ Tuy nhiên với tinh thần trắc nghiệm ta sẽ chuẩn hóa với O là trọng tâm tam giác ABC.