Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông

* Hướng dẫn giải

Đáp án A.

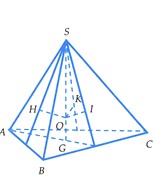
Do SA = SB = SC nên các tam giác SAB, SBC, SCA vuông cân tại S.

Suy ra: S_SAB =  S_SBC = S_SCA

Do SA, SB, SC vuông góc với nhau từng đôi một nên ta có

$V_{S.ABC}=\frac{1}{6}SA.SB.SC=\frac{S{A}^3}{6}=\frac{a^3}{6}\Rightarrow SA=SB=SC=a\Rightarrow AB=BC=CA=a\sqrt{2}$

Gọi O là tâm mặt cầu nội tiếp hình chóp.

Gọi G, H, I, K lần lượt là hình chiều vuông góc của O lên $\left(ABC\right),\left(SAB\right),\left(SBC\right),\left(SCA\right)$ ta có OG=OH=OI=OK=r

Mà $V_{S.ABC}=V_{O.ABC}+V_{O.SAB}+V_{O.SBC}+V_{O.SCA}=\frac{r}{3}\left(3S_{\Delta SAB}+S_{\Delta ABC}\right)$

$=\frac{a^{2}r}{6}\left(3+\sqrt{3}\right)=\frac{a^3}{6}\Rightarrow r=\frac{a}{3+\sqrt{3}}$