Cho các số thực dương x, y thỏa mãn x^2 + x / (x+1) = (y+2)

* Hướng dẫn giải

Chọn đáp án B

Ta có: $x^2+\frac{x}{x+1}=\left(y+2\right)\sqrt{\left(x+1\right)\left(y+1\right)}\iff \frac{x^3+x\left(x+1\right)}{\left(x+1\right)\sqrt{x+1}}=\left(y+2\right)\sqrt{y+1}$

$\mathbf{\iff }{\left(\frac{x}{\sqrt{x+1}}\right)}^{\mathbf{3}}\mathbf{+}\frac{\mathbf{x}}{\sqrt{\mathbf{x}\mathbf{+}\mathbf{1}}}\mathbf{=}{\left(\sqrt{y+1}\right)}^{\mathbf{3}}\mathbf{+}\sqrt{\mathbf{y}\mathbf{+}\mathbf{1}}\left(1\right)$

Xét hàm số $f\left(t\right)=t^3+t,t\in R,f\text{'}\left(t\right)=3t^2+1\ge 0\Rightarrow f\left(t\right)$ đồng biến trên R.

Phương trình (1) trở thành  $f\left(\frac{x}{\sqrt{x+1}}\right)=f\left(\sqrt{y+1}\right)\iff x=\sqrt{\left(x+1\right)\left(y+1\right)}$

Khi đó $P=\left|4-x^2+\sqrt{4-x^2}+a\right|$

Đặt $t=\sqrt{4-x^2}$ , điều kiện $t\in \left[0;2\right]$:

Xét  $f\left(t\right)=t^2+t+a\Rightarrow a\le f\left(t\right)\le a+6,P=\left|f\left(t\right)\right|$

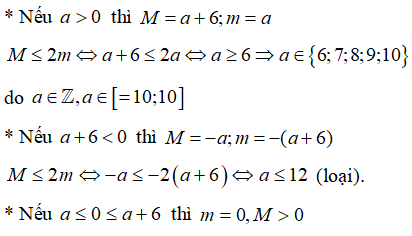
không thỏa mãn điều kiện M$\le$2 .

Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.