Tìm tập hợp các số nguyên n để [ frac{{n - 8}}{{n + 1}} + frac{{n + 3}}{{n + 1}} ] là một số nguyên

* Hướng dẫn giải

Ta có:

\[\begin{array}{l}\frac{{n - 8}}{{n + 1}} + \frac{{n + 3}}{{n + 1}} = \frac{{n - 8 + n + 3}}{{n + 1}} = \frac{{2n - 5}}{{n + 1}} = \frac{{\left( {2n + 2} \right) - 7}}{{n + 1}} = \frac{{2\left( {n + 1} \right) - 7}}{{n + 1}}\\ = \frac{{2\left( {n + 1} \right)}}{{n + 1}} - \frac{7}{{n + 1}} = 2 - \frac{7}{{n + 1}}\end{array}\]

Yêu cầu bài toán thỏa mãn nếu \[\frac{7}{{n + 1}} \in Z\] hay  n + 1 ∈ Ư(7) = {±1; ±7}

Ta có bảng:

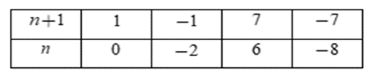
Vậy n ∈ {0; −2; 6; −8}

Đáp án cần chọn là: C