Bài 5 trang 12 sách bài tập Toán lớp 6 Tập 2: Nêu hai cách
Câu hỏi :
Bài 5 trang 12 sách bài tập Toán lớp 6 Tập 2: Nêu hai cách giải thích các phân số sau bằng nhau (dùng khái niệm bằng nhau và dùng tính chất).
* Đáp án
* Hướng dẫn giải
Lời giải:
Cách 1: Dùng khái niệm bằng nhau:
Nếu a . d = b . c thì 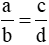 (với a, b, c, d ≠ 0).
(với a, b, c, d ≠ 0).
Cách 2: Dùng tính chất:
- Tính chất 1: Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được phân số bằng phân số đã cho.
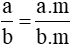 , với m ∈ Z và m ≠ 0.
, với m ∈ Z và m ≠ 0.
- Tính chất 2: Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
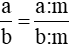 , với n ∈ ƯC (a; b).
, với n ∈ ƯC (a; b).
a) Cách 1 (dùng định nghĩa): vì (−15) . (−11) = 5 . 33 =165 nên 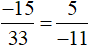 .
.
Vậy 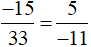
Cách 2 (dùng tính chất 2): Ta có 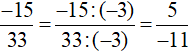 .
.
Vậy 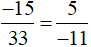
b) Cách 1 (dùng định nghĩa): Vì 7 . (−60) = (−12) . 35 = −420 nên 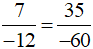 .
.
Vậy 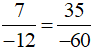 .
.
Cách 2 (dùng tính chất 1): Ta có: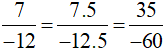
Vậy 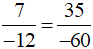 .
.
c) Cách 1 (dùng định nghĩa): Vì (−8) . (−21) = 14 . 12 = 168 nên 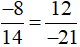
Vậy 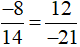
Cách 2 (dùng tính chất 2 và tính chất 1): Ta có: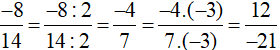
Vậy 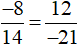
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải SBT Toán 6 Chương 5: Phân số - Bộ Chân trời sáng tạo !!
Copyright © 2021 HOCTAP247
