Một thanh AB hình trụ đặc, đồng chất, có tiết diện S, trọng lượng riêng d, chiều dài L, được giữ thẳng đứng trong môi trường nước có trọng lượng riêng d0. Khoảng cách
Câu hỏi :
Một thanh AB hình trụ đặc, đồng chất, có tiết diện S, trọng lượng riêng d, chiều dài L, được giữ thẳng đứng trong môi trường nước có trọng lượng riêng d0. Khoảng cách từ đầu trên A của thanh đến mặt nước là H0. Người ta thả thanh ra để nó chuyển động đi lên theo phương thẳng đứng. Bỏ qua sức cản của nước và không khí cũng như sự thay đổi của mực nước.
1. Biết rằng kể từ khi thanh bắt đầu nhô lên mặt nước đến khi thanh vừa lên hoàn toàn khỏi mặt nước, lực đẩy Ác-si-mét luôn thay đổi và có giá trị trung bình bằng một nửa lực đẩy Ác-si-mét lớn nhất tác dụng vào vật. Hãy lập biểu thức tính công của lực đẩy Ác-si-mét kể từ lúc thanh AB được thả ra cho đến khi đầu dưới B của thanh lên khỏi mặt nước.
2. Cho d = 6000 N/m3; L = 24 cm; d0 = 10000 N/m3
a) H0 = 12 cm. Tính khoảng cách giữa đầu B và mặt nước khi thanh lên cao nhất.
b) Tìm điều kiện của H0 để thanh có thể lên hoàn toàn khỏi mặt nước
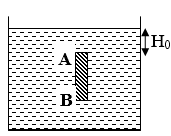
Một thanh AB hình trụ đặc, đồng chất, có tiết diện S, trọng lượng riêng d, chiều dài L, được giữ thẳng đứng trong môi trường nước có trọng lượng riêng d0. Khoảng cách từ đầu trên A của thanh đến mặt nước là H0. Người ta thả thanh ra để nó chuyển động đi lên theo phương thẳng đứng. Bỏ qua sức cản của nước và không khí cũng như sự thay đổi của mực nước.
1. Biết rằng kể từ khi thanh bắt đầu nhô lên mặt nước đến khi thanh vừa lên hoàn toàn khỏi mặt nước, lực đẩy Ác-si-mét luôn thay đổi và có giá trị trung bình bằng một nửa lực đẩy Ác-si-mét lớn nhất tác dụng vào vật. Hãy lập biểu thức tính công của lực đẩy Ác-si-mét kể từ lúc thanh AB được thả ra cho đến khi đầu dưới B của thanh lên khỏi mặt nước.
2. Cho d = 6000 N/m3; L = 24 cm; d0 = 10000 N/m3
a) H0 = 12 cm. Tính khoảng cách giữa đầu B và mặt nước khi thanh lên cao nhất.
b) Tìm điều kiện của H0 để thanh có thể lên hoàn toàn khỏi mặt nước
* Đáp án
* Hướng dẫn giải
Do d0 > d nên lực đẩy Ác-si-mét lớn hơn trọng lượng của thanh Þ thanh chuyển động thẳng đứng đi lên
Ta có: FA = d0.V = d0.S.L (S là tiết diện của thanh)
- Khi thanh bắt đầu chuyển động cho đến khi đầu trên chạm mặt nước, lực đẩy Ác-si-mét không thay đổi. Thanh đi được một đoạn là H0.
- Vậy công trong giai đoạn này là:A1=d0.S.L.H0...................................................
Khi đầu trên của thanh bắt đầu nhô khỏi mặt nước thì lực Ác-si-mét giảm dần đến bằng 0 cho tới khi đầu dưới lên khỏi mặt nước. Quãng đường đi trong giai đoạn này là L.
Vậy: A2 = .d0.S.L2..........................................................
- Công của lực đẩy Ác-si-mét trong toàn bộ quá trình là:
AA = A1 + A2 = d0.S.L.H0 + .d0.S.L2.................................................Công của trọng lực thực hiện trong cả quá trình có độ lớn là:
A = P(H0 + L + h)
Mà P là trọng lượng của thanh: P = d.S.L
Þ A = d.S.L(H0 + L + h)......................................................................
Theo định luật bảo toàn năng lượng: A = AA
Þ d.S.L(H0 + L + h) = d0.S.L.H0 + ![]() d0.S.L2
d0.S.L2
Þ......................
Thay số: h = 4 cm. ................................................................................Để thanh ra khỏi mặt nước thì h ³ 0
Þ
Þ .................................................................................
thay số: H0 ³ 6 cm.................................................................................Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi Vật lí ôn vào 10 hệ chuyên có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
