Tại hai địa điểm A và B trên một đường thẳng, lúc 6 giờ có hai xe chuyển động, một xe xuất phát tại A và một xe xuất phát tại

Câu hỏi :

Tại hai địa điểm A và B trên một đường thẳng, lúc 6 giờ có hai xe chuyển động, một xe xuất phát tại A và một xe xuất phát tại B theo hướng AB với vận tốc không đổi. Nếu xuất phát cùng lúc thì hai xe gặp nhau tại điểm C sau 3 giờ chuyển động, nếu xe tại A xuất phát chậm 10 phút thì hai xe gặp nhau tại D. Biết AB = 30km, CD = 20km. Hãy xác định:

          a. Vận tốc của mỗi xe.

           b. Thời điểm hai xe gặp nhau tại C và D.

* Đáp án

* Hướng dẫn giải

a. Gọi v₁ là vận tốc xe đi từ A, v₂ là vận tốc xe đi từ B.

- Chuyển động lần 1: v₁t - v₂t = 30  

     => v₁ - v₂ = 30/t = 10 (1)

- Chuyển động lần 2:

 v₁t₁ = v₁t + 20   => t₁ = (v₁t + 20)/v₁

                                t₁ = (3v₁ + 20)/v₁ (2)

 (v₂t₁ + v₂/6) - v₂t = 20

    => t₁ = (20 - v₂/6 + 3v₂)/v₂

Từ 1, 2, 3 có phương trình: v₂² + 10v₂ - 1200 = 0;

- Giải phương trình tính được v₂ = 30km/h => v₁ = 40km/h.

 Vận tốc của xe tại A là v₁ = 40km/h; của xe tại B là v₂ = 30km/h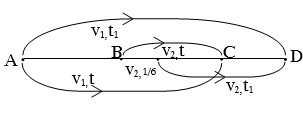

 b.

- Gặp nhau lần đầu tại C lúc: 6 giờ + 3 giờ = 9 giờ 00

- Thời gian gặp lần sau: t₁ = (3.40 + 20)/40 = 3 giờ 30 phút

- Lúc đó là: 6 giờ + 3 giờ 30 phút + 10 phút = 9 giờ 40 phút