Một người đứng tại điểm A trên bờ hồ phẳng lặng (hình vẽ
Câu hỏi :
Một người đứng tại điểm A trên bờ hồ phẳng lặng (hình vẽ), người này muốn tới điểm B trên mặt hồ. Khoảng cách từ b tới bờ hồ là BC = d, khoảng cách AC = S, người đó chỉ có thể bơi thẳng đều trên mặt nước với vận tốc v1 và chạy thẳng đều dọc theo bờ hồ với vận tốc là v2 (v1 < v2). Tìm quãng đường mà người náy phải đi để khoảng thời gian đi từ A đến B là nhỏ nhất.
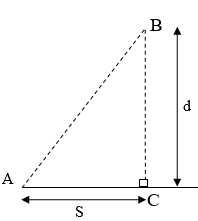
Một người đứng tại điểm A trên bờ hồ phẳng lặng (hình vẽ), người này muốn tới điểm B trên mặt hồ. Khoảng cách từ b tới bờ hồ là BC = d, khoảng cách AC = S, người đó chỉ có thể bơi thẳng đều trên mặt nước với vận tốc v1 và chạy thẳng đều dọc theo bờ hồ với vận tốc là v2 (v1 < v2). Tìm quãng đường mà người náy phải đi để khoảng thời gian đi từ A đến B là nhỏ nhất.

* Đáp án
* Hướng dẫn giải
+ Gọi quãng đường DC có độ dài là: x
+ Độ dài quãng đường BD:
+ Thời gian người này đi từ A đến D rồi đến B là:
t = tAD + tDB =
+ Khi đó:
Khi đó =
v12v22t2 – 2Sv12v2t + s2v12 + v12d2 – v22d2 >= 0
v1v2d
+ Dẫn đến t ![]()
+ Đạt tại x =
+ Quãng đường mà người nay phải đi thỏa mãn yêu cầu bài toán là :
SAD + SDB = S – x +
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi Vật lí ôn vào 10 hệ chuyên có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
