Hai xe ô tô khởi hành cùng một lúc tại điểm A
Câu hỏi :
Hai xe ô tô khởi hành cùng một lúc tại điểm A. Xe thứ nhất chạy một vòng trên các cạnh của tam giác đều ABC (AB= a= 300m) theo chiều từ A đến B (Hình 2). Khi đến B xe nghỉ 4 phút, đến C xe nghỉ 6 phút, vận tốc của xe trên mỗi cạnh là không đổi nhưng khi xe chuyển động trên cạnh kế tiếp thì vận tốc tăng gấp 2 lần so với trước. Biết vận tốc trung bình của xe thứ nhất là 0,8m/s. Xe thứ hai chạy liên tục nhiều vòng trên các cạnh của tam giác ABC theo chiều từ A đến C với vận tốc không đổi là 3m/s.
a. Hỏi xe thứ nhất đi được một vòng thì gặp xe thứ hai mấy lần?
b. Xác định các vị trí hai xe gặp nhau.
c. Vẽ đồ thị vị trí của hai xe theo thời gian.
Hai xe ô tô khởi hành cùng một lúc tại điểm A. Xe thứ nhất chạy một vòng trên các cạnh của tam giác đều ABC (AB= a= 300m) theo chiều từ A đến B (Hình 2). Khi đến B xe nghỉ 4 phút, đến C xe nghỉ 6 phút, vận tốc của xe trên mỗi cạnh là không đổi nhưng khi xe chuyển động trên cạnh kế tiếp thì vận tốc tăng gấp 2 lần so với trước. Biết vận tốc trung bình của xe thứ nhất là 0,8m/s. Xe thứ hai chạy liên tục nhiều vòng trên các cạnh của tam giác ABC theo chiều từ A đến C với vận tốc không đổi là 3m/s.
a. Hỏi xe thứ nhất đi được một vòng thì gặp xe thứ hai mấy lần?
b. Xác định các vị trí hai xe gặp nhau.
c. Vẽ đồ thị vị trí của hai xe theo thời gian.
* Đáp án
* Hướng dẫn giải
Gọi v, 2v, 3v là vận tốc của xe 1 trên AB, BC, CA.
- Thời gian xe 1 đi hết một vòng:
Mà
- Thời gian xe 1 đi trên cạnh AB, BC, CA: t1=300s; t2=150s; t3=75s.
- Lập bảng
Xe 1:
|
Thời điểm t(s) |
0 |
300 |
300 ® 540 |
690 |
690 ® 1050 |
1125 |
|
Vị trí |
A |
B |
B |
C |
C |
A |
Xe 2:
|
Thời điểm tx100(s) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Vị trí |
A |
C |
B |
A |
C |
B |
A |
C |
B |
A |
C |
B |
A |
- So sánh hai bảng:
+ Trong giây thứ 200 ® 300 xe 1 đi từ A ® B, xe 2 đi từ B ® A hai xe gặp nhau lần thứ nhất tại điểm M trên đoạn AB
Sau 200s xe (1) đi được AH = vt = 200m ® HB = 100m
Trong thời gian xe (1) và (2) cùng đi từ H ® M và B ® M
® ,
+ Tại thời điểm 500s xe 1 đang nghỉ tại B và xe 2 đến B nên hai xe gặp nhau lần thứ 2 tại B.
+ Thời điểm 700s xe 2 tới C, xe 1 nghỉ tại C. Vậy hai xe gặp nhau lần thứ 3 tại điểm C.
+ Giây thứ 1000 xe 2 tới C, xe 1 đang nghỉ tại C. Vậy hai xe gặp nhau lần thứ 4 tại C.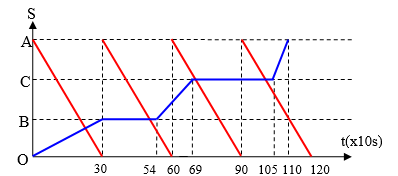
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi Vật lí ôn vào 10 hệ chuyên có đáp án (Mới nhất) !!
Copyright © 2021 HOCTAP247
