Tính khoảng cách OA, OA/ và OF của thấu kính.
Câu hỏi :
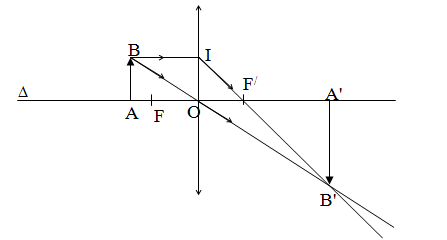
Vật sáng AB qua một thấu kính cho ảnh A’B’ như hình vẽ..png)
* Đáp án
* Hướng dẫn giải
a) Thấu kính đã cho là thấu kính hội tụ, vì ảnh A'B' là ảnh thật (ngược chiều).
b) Nêu cách vẽ hình
- Nối B với B’cắt trục chính tại quang tâm O.
- Dựng TKHT vuông góc với trục chính tại O.
- Vẽ tia tới BI song song với trục chính, tia ló đi qua B’ và cắt trục chính tại tiêu điểm F’.
- Lấy F trên trục chính đối xứng với F’ qua O
c) \(\Delta OAB\) và \(\Delta OA'B'\) đồng dạng:
\(\frac{{AB}}{{A'B'}} = \frac{{OA}}{{OA'}} \Leftrightarrow \frac{5}{{10}} = \frac{{OA}}{{OA'}} \Rightarrow OA' = 2OA\)
Ta có AA' = OA + OA' = 90
⇒ OA + 2.OA = 90 (cm)
\( \Rightarrow OA = \frac{{90}}{3} = 30\) (cm)
\( \Rightarrow OA' = 2OA = 2.30 = 60\) (cm)
\(\Delta OIF'\) và \(\Delta A'B'F'\) đồng dạng, suy ra:
\(\frac{{OI}}{{A'B'}} = \frac{{OF'}}{{A'F'}} \Leftrightarrow \frac{{AB}}{{A'B'}} = \frac{{OF'}}{{OA' - OF'}} \Leftrightarrow \frac{5}{{10}} = \frac{{OF'}}{{60 - OF'}}\)
\( \Rightarrow OF' = OF = 20\) (cm)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề kiểm tra 1 tiết môn Vật lý 9 HK2 năm 2019 trường THCS Nguyễn Văn Trỗi
Copyright © 2021 HOCTAP247
