b) Thực hiện thí nghiệm Dụng cụ + 2 gương phẳng nhỏ. + 1 thước chia độ

Câu hỏi :

b) Thực hiện thí nghiệm

Dụng cụ

+ 2 gương phẳng nhỏ.

+ 1 thước chia độ bằng bìa.

+ 2 đoạn ống hút khoảng 4 cm.

Tiến hành

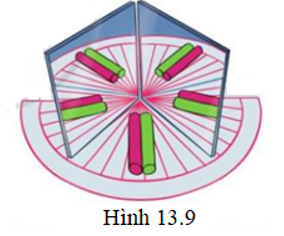
Đặt hai gương vuông góc với thước chia độ sao cho hai gương hợp với nhau một góc nhọn. Đặt ống hút trong góc tạo bởi hai gương (hình 13.9). Thay đổi góc giữa các gương và đếm số ảnh được tạo bởi hệ gương rồi ghi kết quả như bảng dưới đây.

Góc giữa hai gương $\left(\alpha \right)$	$\alpha$	30o	40o	50o	60o	70o	80o	90o
Số ảnh (n)	n

Từ số liệu vừa thu được, em có thể dự đoán công thức liên hệ giữa $\alpha$ và n không? Nếu có, em hãy ghi lại biểu thức đó.

* Đáp án

* Hướng dẫn giải

b. Tiến hành thí nghiệm thu được bảng số liệu sau:

Góc giữa hai gương $\left(\alpha \right)$	$\alpha$	30o	40o	50o	60o	70o	80o	90o
Số ảnh (n)	n	11	8	6	5	4	3	3

Công thức liên hệ giữa $\alpha$ và n có dạng: $n=2k-1$với $\frac{360}{\alpha }=2k\left(k\in N\right)$

Chứng minh:

Chú ý: Mỗi gương phẳng sẽ tạo ra một mặt phẳng tới (do đường thẳng chứa gương tạo thành), có ảnh của vật qua gương khi vật nằm trong mặt phẳng tới. Nếu vật không nằm trong mặt phẳng tới sẽ không tạo ra ảnh.

Sơ đồ tạo ảnh qua hệ:

$\begin{array}{l}A\stackrel{\left(M\right)}{\to }{A}_1\stackrel{\left(N\right)}{\to }{A}_3\stackrel{\left(M\right)}{\to }{A}_5\stackrel{\left(N\right)}{\to }\mathrm{...}\\ A\stackrel{\left(N\right)}{\to }{A}_2\stackrel{\left(M\right)}{\to }{A}_4\stackrel{\left(N\right)}{\to }{A}_6\stackrel{\left(M\right)}{\to }\mathrm{...}\end{array}$

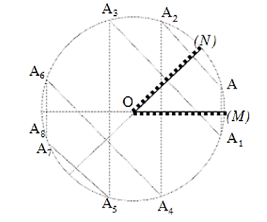
Từ bài toán ta có thể biểu diễn một số trường hợp đơn giản. Theo hình vẽ ta có:

$\widehat{A_{1}O{A}_2}=2\alpha$

$\widehat{A_{3}O{A}_4}=4\alpha$

….

$\widehat{A_{2k-1}O{A}_{2k}}=2k\alpha$

Theo điều kiện bài toán thì $\frac{360}{\alpha }=2k\left(k\in N\right)$ 

$\Rightarrow 2k\alpha ={360}^o.$ Vậy góc $\widehat{A_{2k-1}O{A}_{2k}}=2k\alpha ={360}^o$

Tức là ảnh A_2k-1 và ảnh A_2k trùng nhau.

Trong hai ảnh này có một ảnh sau gương (M) và một ảnh sau gương (N) nên không tiếp tục cho ảnh nữa.

Vậy số ảnh của A cho bởi hai gương là: n = 2k – 1 ảnh.