Hai hình vuông ABCD và BMNC đều có cạnh bằng 3cm và xếp
Câu hỏi :
Hai hình vuông ABCD và BMNC đều có cạnh bằng 3cm và xếp thành hình chữ nhật AMND. Cho biết hình tứ giác BMCD là hình bình hành. Tính diện tích hình bình hành BMCD bằng các cách khác nhau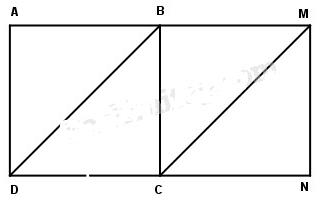
* Đáp án
* Hướng dẫn giải
Cách 1:
Vì tứ giác ABCD, BMNC đều là hình vuông mà tứ giác BNMC là hình bình hàng suy ra đường cao h cũng chính là cạnh BC và độ dài đáy cũng chính là cạnh DC.
Diện tích hình bình hành BMCD là:
S = a x h = DC x BC = 3 x 3 = 9 (cm2)
Đáp số: 9cm2
Cách 2: Diện tích hình bình hành BMCD bằng diện tích tam giác BCD cộng với diện tích tam giác BCM.
Tam giác BCD có đường cao BC = 3cm, cạnh đá DC = 3cm
Diện tích tam giác BCD là:
SBCD = độ dài đáy x đường cao : 2
= DC x BC : 2 = 3 x 3 : 2 = 4,5 cm2
Tam giác BCM có đường cao CB = 3cm, cạnh đáy BM = 3cm
Diện tích tam giác BCM là:
SBCM = độ dài đáy x đường cao : 2
= CB x BM : 2 = 3 x 3 : 2 = 4,5 cm2
Diện tích hình bình hành BMCD là:
S = SBCD + SBCM = 4,5 + 4,5 = 9 cm2
Cách 3:
Diện tích hình bình hành BMCD bằng diện tích nửa hình vuông ABCD + diện tích nửa hình vuông BMNC.
Diện tích nửa hình vuông ABCD có cạnh bằng 3cm là:
3 x 3 : 2 = 4,5 cm2
Diện tích nửa hình vuông BMNC có cạnh bằng 3cm là:
3 x 3 : 2 = 4,5 cm2
Diện tích hình bình hành BMCD là:
S = 4,5 + 4,5 = 9 cm2
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải vở bài tập Toán lớp 4 Bài 113: Luyện tập chung có đáp án !!
Copyright © 2021 HOCTAP247
