Cho hình chóp S.ABC, đáy là tam giác vuông tại B, cạnh bên SA vuông góc với mặt đáy. Biết SA = AB = BC và diện tích

* Hướng dẫn giải

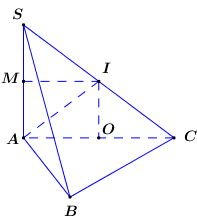
Gọi O là trung điểm của AC. Vì tam giác ABC vuông tại B nên O là tâm đường tròn ngoại tiếp tam giác ABC.

Gọi I, M là trung điểm của SC, SA. Ta có IO là đường trung bình của tam giác SAC $\Rightarrow IO//SA$.

Mà $SA\perp \left(ABC\right)\Rightarrow IO\perp \left(ABC\right)\Rightarrow IO$ là trực của (ABC)$\Rightarrow IA=IB=IC$.

Lại có IM là đường trung bình của tam giác SAC nên IM // AC $\Rightarrow IM\perp SA$$\Rightarrow IM$ là trung trực của SA, do đó $IS=IA$.

$\Rightarrow IA=IB=IC=IS$ \[ \Rightarrow I\] là tâm mặt cầu ngoại tiếp chóp SABC.

⇒ Bán kính của mặt cầu ngoại tiếp chóp S.ABC là $R=\frac{1}{2}SC$.

Ta lại có \[4\pi {R^2} = 3\pi \Leftrightarrow R = \frac{{\sqrt 3 }}{2} \Rightarrow SC = \sqrt 3 \].

Đặt $SA=AB=BC=x$, ta có tam giác SAB vuông cân tại A nên $SB=x\sqrt{2}$.

Ta có: $\{\begin{array}{l}BC\perp AB\\ BC\perp SA\end{array}\Rightarrow BC\perp \left(SAB\right)\Rightarrow BC\perp SB$$\Rightarrow \Delta SBC$ vuông tại B.

\[ \Rightarrow S{B^2} + B{C^2} = S{C^2} \Rightarrow 2{x^2} + {x^2} = 3 \Leftrightarrow x = 1\]

Vậy thể tích khối chóp là $V=\frac{1}{3}SA.S_{\Delta ABC}=\frac{1}{3}SA.\frac{1}{2}AB.BC=\frac{1}{6}{x}^3=\frac{1}{6}$.

Đáp án C.