Cho hình lăng trụ đứng ABC.A’B’C’. Đáy là tam giác vuông tại A, có BC = 2AC = 2a. Đường thẳng AC’ tạo với

* Hướng dẫn giải

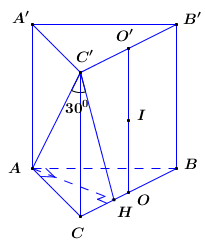
Gọi O, O’ lần trung điểm của BC và B’C’.

Vì tam giác ABC, A’B’C’ lần lượt vuông tại A và A’ nên O, O’ lần lượt là tâm mặt cầu ngoại tiếp tam giác ABC, A’B’C’. Lại có OO’ vuông góc với hai đáy nên OO’ là trục hai đáy.

Gọi I là trung điểm của OO’ =>I là tâm mặt cầu ngoại tiếp khối lăng trụ.

Trong (ABC) kẻ $AH\perp BC(H\in BC)$ ta có $\{\begin{array}{l}AH\perp BC\\ AH\perp B{B}^{\text{'}}\end{array}\Rightarrow AH\perp \left(BC{C}^{\text{'}}{B}^{\text{'}}\right)\Rightarrow H{C}^{\text{'}}$ là hình chiếu của AC’ lên (BCC’B’), do đó $\angle (A{C}^{\text{'}};\left(BC{C}^{\text{'}}{B}^{\text{'}}\right))=\angle (A{C}^{\text{'}};HC)=\angle A{C}^{\text{'}}H={30}^0$.

Xét tam giác vuông ABC ta có $AB=\sqrt{B{C}^2-A{C}^2}=\sqrt{4a^2-a^2}=a\sqrt{3}$$\Rightarrow AH=\frac{AB.AC}{BC}=\frac{a\sqrt{3}.a}{2a}=\frac{a\sqrt{3}}{2}$.

Xét tam giác AC’H vuông tại H có: $A{C}^{\text{'}}=\frac{AH}{\sin {30}^0}=\frac{a\sqrt{3}}{2}:\frac{1}{2}=a\sqrt{3}$.

Xét tam giác vuông AA’C’ có: $A{A}^{\text{'}}=\sqrt{A{C^{\text{'}}}^2-A^{\text{'}}{C^{\text{'}}}^2}=\sqrt{3a^2-a^2}=a\sqrt{2}=O{O}^{\text{'}}$$\Rightarrow IO=\frac{1}{2}O{O}^{\text{'}}=\frac{a\sqrt{2}}{2}$.

Xét tam giác vuông IOC có: \[IC = \sqrt {I{O^2} + O{C^2}} = \sqrt {\frac{{{a^2}}}{2} + {a^2}} = \frac{{a\sqrt 6 }}{2} = R\].

Vậy diện tích mặt cầu ngoại tiếp khối lăng trụ là: $S=4\pi R^2=4\pi .{\left(\frac{a\sqrt{6}}{2}\right)}^2=6\pi a^2$.

Đáp án B.