Cho hàm số f(x) liên tục trên R, có bảng biến thiên như hình vẽ dưới đây: Đặt g(x)=|m+f(x+1)| (m là tham số).

* Hướng dẫn giải

Dựa vào BBT ta thấy $f^{\text{'}}\left(x\right)=0\iff [\begin{array}{l}x=x_1\\ x=x_2\end{array}$.

Đặt $h\left(x\right)=m+f(x+1)$ ta có \[h'\left( x \right) = f'\left( {x + 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x + 1 = {x_1}}\\{x + 1 = {x_2}}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = {x_1} - 1}\\{x = {x_2} - 1}\end{array}} \right.\], do đó hàm số $h\left(x\right)=m+f(x+1)$có 2 điểm cực trị.

Suy ra để hàm số $g\left(x\right)=\left|h\left(x\right)\right|=|m+f(x+1)|$ có đúng 3 điểm cực trị thì phương trình $m+f(x+1)=0$ phải có nghiệm bội lẻ duy nhất.

Ta có: $m+f(x+1)=0\iff f(x+1)=-m$, dựa vào BBT ta thấy đường thẳng 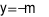cắt qua (không tính điểm tiếp xúc) đồ thị hàm số $y=f(x+1)$ tại 1 điểm duy nhất khi và chỉ khi $[\begin{array}{l}-m\ge 1\\ -m\le -3\end{array}\iff [\begin{array}{l}m\le -1\\ m\ge 3\end{array}$.

Đáp án C.