Trang chủ
Đề thi & kiểm tra
Toán học
30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải !!
Cho hình chóp S.ABCD có đáy ABCD là hình chữ...
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I,SA vuông góc với đáy
Câu hỏi :
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm I,SA vuông góc với đáy. Điểm cách đều các đỉnh của hình chóp là:
C. Điểm nằm trên đường thẳng d//SA và không thuộc SC.
D.
A. Tập xác định của hàm số là
B. Tập giá trị của hàm số là
C. Tập giá trị của hàm số là
D. Tập xác định của hàm số là
* Đáp án
D
* Hướng dẫn giải
Chọn D
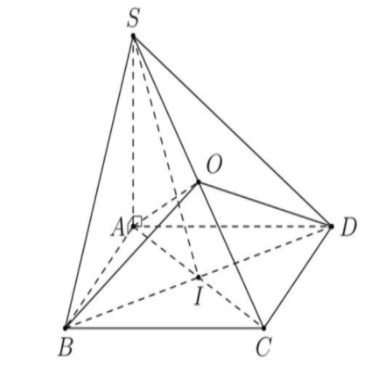
Gọi O là trung điểm SC Vì ABCD là hình chữ nhật nên
Tam giác SBC,SDC,SAC lần lượt vuông tại B,D,A nên OA=OB=OC=OD=OS
Vậy O là điểm cách đều của hình chóp.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
30 đề thi thử THPT Quốc gia môn Toán năm 2022 có lời giải !!
Số câu hỏi: 81
Copyright © 2021 HOCTAP247
