Cho hình lăng trụ đứng ABC.A'B'C' có điểm O và G lần lượt là tâm của mặt bên ABB'A' và trọng tâm của ABC.

* Hướng dẫn giải

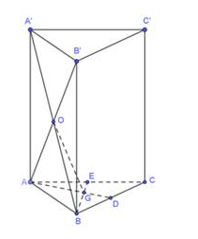
Ta có:

\(d\left( {O,\left( {ABC} \right)} \right) = \frac{1}{2}AA'\)

\({S_{\Delta AOB}} = \frac{1}{2}d\left( {G;AB} \right).AB\) mà \(d\left( {G;AB} \right) = \frac{1}{3}d\left( {C;AB} \right).\) Khi đó \({S_{\Delta AGB}} = \frac{1}{3}{S_{\Delta ABC}}\)

Vậy: \({V_{OAGB}} = \frac{1}{{18}}{V_{ABC.A'B'C'}} = \frac{1}{{18}}.270 = 15c{m^3}\) nên chọn đáp án C.