Cho hình chóp tứ giác đều S.ABCD có SA = AB = a. Góc giữa SA và CD là

* Hướng dẫn giải

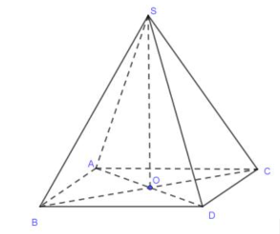
Vì \(AB//CD\) nên \(\left( {\widehat {SA;CD}} \right) = \left( {\widehat {SA;AB}} \right)\) mà \(S.ABCD\) là chóp tứ giác đều và \(SA = AB = a\) nên \(\Delta SAB\) đều. Vậy \(\widehat {\left( {SA;AB} \right)} = {60^0},\) khi đó góc giữa \(SA\) và \(CD\) là \({60^0}\) nên chọn đáp án A.