Cho hình chóp S.ABC có AB = AC = 5a;BC = 6a. Các mặt bên tạo với đáy góc 60^0. Tính thể tích khối chóp S.ABC

* Hướng dẫn giải

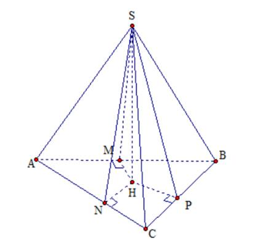
Gọi \(H\) là hình chiếu của \(S\) trên mặt phẳng \(\left( {ABC} \right).\) Các điểm \(M,N,P\) lần lượt là hình chiếu của \(H\) trên các cạnh \(AB,AC,BC.\)

Khi đó ta có: \(\widehat {SMH} = \widehat {SNH} = \widehat {SPH} = {60^0},\) suy ra: \(HM = HN = HP\) hay \(H\) là tâm đường tròn nội tiếp tam giác \(ABC.\)

Xé tam giác \(ABC\) ta có:

Nửa chu vi: \(p = \frac{{AB + BC + CA}}{2} = \frac{{5a + 5a + 6a}}{2} = 8a.\)

Diện tích: \({S_{\Delta ABC}} = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \sqrt {8a.3a.3a.2a} = 12{a^2}.\)

Áp dụng công thức \(S = pr \Rightarrow r = \frac{S}{p} = \frac{{12{a^2}}}{{8a}} = \frac{{3a}}{2}.\)

Suy ra: \(HM = r = \frac{{3a}}{2},SH = HM.\tan {60^0} = \frac{{3a}}{2}.\sqrt 3 = \frac{{3\sqrt 3 a}}{2}.\)

Vậy \({V_{ABC}} = \frac{1}{3}{S_{\Delta ABC}}.SH = \frac{1}{3}.12{a^2}.\frac{{3\sqrt 3 a}}{2} = 6\sqrt 3 {a^3}.\)

Đáp án A.