Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, AB =căn 3 ,AD = căn 7 . Hai mặt bên ABB'A' và ADD'A'

* Hướng dẫn giải

\(AH = h\)

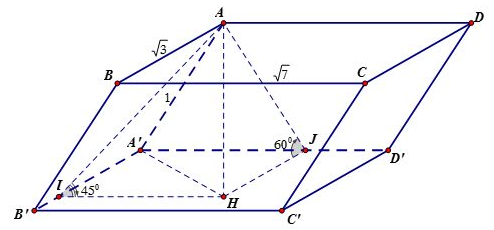
Gọi \(H\) là hình chiếu của \(A\) trên đáy \(\left( {A'B'C'D'} \right)\) suy ra là chiều cao

Gọi \(I\) là hình chiếu của \(A\) trên \(A'B' \Rightarrow \widehat {AIH} = {45^0}\)

Gọi \(J\) là hình chiếu của \(A\) trên \(A'D' \Rightarrow \widehat {AJH} = {60^0}\)

Ta có \(\Delta AIH\) vuông cân tại \(H \Rightarrow IH = AH = h\)

\(\Delta AJH\) vuông tại \(H \Rightarrow JH = \frac{h}{{\tan {{60}^0}}} = \frac{{h\sqrt 3 }}{3}\)

Tứ giác \(A'JHI\) là hình chữ nhật \( \Rightarrow A'H = \frac{{2h\sqrt 3 }}{3}\)

\(\Delta AA'H\) vuông tại \(H \Rightarrow 1 = {h^2} + {\left( {\frac{{2h\sqrt 3 }}{3}} \right)^2} \Rightarrow h = \frac{{\sqrt {21} }}{7}\)

\({S_{ABCD}} = AB.AD = \sqrt {21} \)

\( \Rightarrow V = {S_{ABCD}}.h = \sqrt {21} .\frac{{\sqrt {21} }}{7} = 3\)

Đáp án D.