Cho hình chóp tứ giác S.ABCD có SA = x và tất cả các cạnh còn lại đều bằng 1. Khi thể tích khối chóp S.ABCD đạt

* Hướng dẫn giải

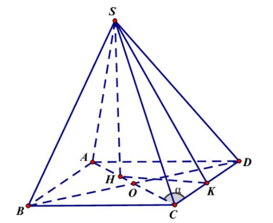
Gọi

\(H\)là tâm đường tròn ngoại tiếp tam giác \(BCD,\) do \(SB = SC = SD\) nên \(SH\) là trục của đường tròn ngoại tiếp tam giác \(BCD,\) suy ra \(SH \bot \left( {ABCD} \right).\)

Do tứ giác \(ABCD\) là hình thoi nên \(AC\) là đường trung trực của đường thẳng \(BD\) do đó \(H \in AC.\)

Đặt \(\alpha = \widehat {ACD},0 < \alpha < \frac{\pi }{2} \Rightarrow \widehat {BCD} = 2\alpha ,\) suy ra \({S_{ABCD}} = 2{S_{BCD}} = BC.CD.\sin \widehat {BCD} = \sin 2\alpha .\)

Gọi \(K\) là trung điểm của \(CD \Rightarrow CD \bot SK,\) mà \(CD \bot SH\) suy ra \(CD \bot HK.\)

\(HC = \frac{{CK}}{{\cos \alpha }} = \frac{1}{{2\cos \alpha }},SH = \sqrt {S{C^2} - H{C^2}} = \sqrt {1 - \frac{1}{{4{{\cos }^2}\alpha }}} = \frac{{\sqrt {4{{\cos }^2}\alpha - 1} }}{{2\cos \alpha }}\).

Thể tích khối chóp \(S.ABCD\) là \(V = \frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}\frac{{\sqrt {4\cos \alpha - 1} }}{{2\cos \alpha }}.\sin 2\alpha = \frac{1}{3}\sin \alpha \sqrt {4{{\cos }^2}\alpha - 1} \)

Do đó \(V = \frac{1}{6}\left( {2\sin \alpha } \right)\sqrt {4{{\cos }^2}\alpha - 1} \le \frac{1}{6}\frac{{4{{\sin }^2}\alpha + 4{{\cos }^2}\alpha - 1}}{2} = \frac{1}{4}.\)

Dấu “=” xảy ra khi \(2\sin \alpha = \sqrt {4{{\cos }^2}\alpha - 1} \Leftrightarrow 4{\sin ^2}\alpha = 4{\cos ^2}\alpha - 1 \Leftrightarrow {\cos ^2}\alpha = \frac{5}{8}\)

\( \Leftrightarrow \cos \alpha = \frac{{\sqrt {10} }}{4}.\) Khi đó \(HC = \frac{2}{{\sqrt {10} }},SH = \frac{{\sqrt {15} }}{5}.\)

Gọi \(O = AC \cap BD,\) suy ra \(AC = 2OC = 2CD.\cos \alpha = \frac{{\sqrt {10} }}{2}.\)

\(AH = AC - HC = \frac{{\sqrt {10} }}{2} - \frac{2}{{\sqrt {10} }} = \frac{3}{{\sqrt {10} }}.\)

Vậy \(x = SA = \sqrt {S{H^2} + A{H^2}} = \sqrt {\frac{3}{5} + \frac{9}{{10}}} = \frac{{\sqrt 6 }}{2}.\)

Đáp án D.