Cho hai số thực a,b thỏa mãn 1 >a>=b>0. Tìm giá trị nhỏ nhất của biểu thức sau T=(loga(b))^2+logab(a^36)

* Hướng dẫn giải

Ta có \(T = \log _a^2b + {\log _{ab}}{a^{36}}\)

\( = \log _a^2b + 36.\frac{1}{{{{\log }_a}ab}}\)

\( = \log _a^2b + \frac{{36}}{{1 + {{\log }_a}b}}\)

Đặt \(t = {\log _a}b\)

Vì \(0 < b \le a < 1\) nên \({\log _a}b \ge {\log _a}a \Rightarrow t \ge 1.\)

Xét hàm \(f\left( t \right) = {t^2} + \frac{{36}}{{1 + t}}\) trên \(\left[ {1; + \infty } \right)\)

\(f'\left( t \right) = 2t - \frac{{36}}{{{{\left( {t + 1} \right)}^2}}},f'\left( t \right) = 0 \Leftrightarrow t = 2\)

Bảng biến thiên

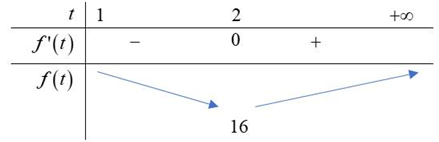
Từ bảng biến thiên ta có \({T_{\min }} = 16\)

Dấu “=” xảy ra \( \Leftrightarrow t = 2 \Leftrightarrow b = {a^2}.\)

Đáp án C