Cho hình lăng trụ tam giác đều (ABC.A'B'C' ) có (AB = a, ) góc giữa đường thẳng (A'C ) và mặt phẳng ( left( {ABC} right) ) bằng ({45^0}. ) Thể tích của khối lăng trụ (ABC.A'B'C' )...

* Hướng dẫn giải

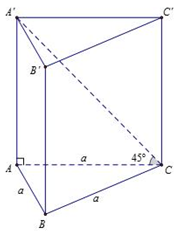
+ Ta có \(AA' \bot \left( {ABC} \right)\) nên \(\left( {\widehat {A'C,\left( {ABC} \right)}} \right) = \widehat {\left( {A'C,AC} \right)} = \widehat {A'CA} = {45^0}.\) Khi đó:

\(\tan {45^0} = \frac{{AA'}}{{AC}} \Rightarrow AA' = AC.\tan {45^0} = a.\)

+ \({S_{ABC}} = \frac{1}{2}.AB.AC.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}.\)

+ Vậy \({V_{ABC.A'B'C'}} = {S_{ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{4}.\)

Đáp án B