Trang chủ
Đề thi & kiểm tra
Toán học
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Cho tứ diện (OABC ) có (OA,OB,OC ) đôi một...
Cho tứ diện (OABC ) có (OA,OB,OC ) đôi một vuông góc và (OA = OB = OC = a. ) Khi đó thể tích của khối tứ diện (OABC ) là
Câu hỏi :
Cho tứ diện \(OABC\) có \(OA,OB,OC\) đôi một vuông góc và \(OA = OB = OC = a.\) Khi đó thể tích của khối tứ diện \(OABC\) là
A.\(\frac{{{a^3}}}{2}.\)
B.\(\frac{{{a^3}}}{{12}}.\)
C.\(\frac{{{a^3}}}{6}.\)
D. \(\frac{{{a^3}}}{3}.\)
* Đáp án
C
* Hướng dẫn giải
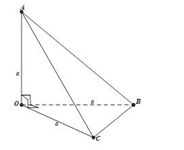
Ta có: \(V = \frac{1}{3}{S_{OBC}}.OA = \frac{1}{3}.\frac{1}{2}.OB.OC.OA = \frac{{{a^3}}}{6}.\)
Đáp án C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Số câu hỏi: 1497
Copyright © 2021 HOCTAP247
