Cho hình chóp (S.ABCD ) có đáy là hình chữ nhật với , (BC = 4a ), (SA = 12a ) và (SA ) vuông góc với đáy. Tính bán kính (R ) của mặt cầu ngoại tiếp hình chóp (S.ABCD ).

* Hướng dẫn giải

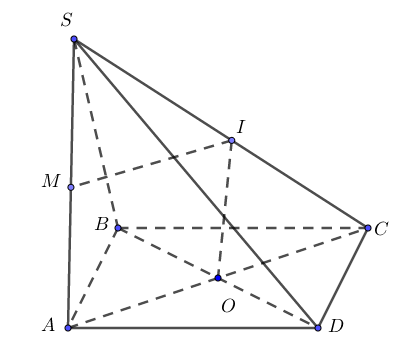
* Gọi \(O\)là tâm của hình chữ nhật \(ABCD.\) Dựng đường thẳng \(Ox\) vuông góc mặt phẳng đáy, ta có \(Ox//SA \Rightarrow Ox \cap SC = I.\) Dễ thấy, \(I\) là trung điểm của \(SC,\) cách đều các đỉnh \(S,A,C\) và là tâm của mặt cầu ngoại tiếp hình chóp \(S.ABCD,\) ta có \(R = \frac{{SC}}{2}.\)

* Xét tam giác \(ABC:AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {9{a^2} + 16{a^2}} = 5a.\)

Xét tam giác \(SAC:SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {144{a^2} + 25{a^2}} = 13a.\)

Vậy \(R = \frac{{SC}}{2} = \frac{{13a}}{2}.\)

Đáp án A