Cho hàm số (y = f(x) ) có đồ thị như hình sau:Đồ thị hàm số (g(x) = frac{{2020}}{{2f(x) + 1}} ) có số đường tiệm cận đứng là:A.2.C. 4.D.5.

* Hướng dẫn giải

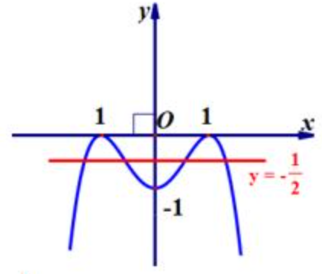
Ta có \(2f\left( x \right) + 1 = 0 \Leftrightarrow f\left( x \right) = - \frac{1}{2}.\)

Từ đồ thị ta có phương trình này có 4 nghiệm \({x_1},{x_2},{x_3},{x_4}.\)

Xét giới hạn \(\mathop {\lim }\limits_{x \to {x_i}} g\left( x \right) = \mathop {\lim }\limits_{x \to {x_i}} \frac{{2020}}{{2f\left( x \right) + 1}} = \infty \) do đó \(x = {x_i}\left( {i = 1,2,3,4} \right)\) đều là các tiệm cận đứng của đồ thị hàm số \(y = g\left( x \right) = \frac{{2020}}{{2f\left( x \right) + 1}}.\)

Vậy đồ thị hàm số \(y = g\left( x \right) = \frac{{2020}}{{2f\left( x \right) + 1}}\) có 4 đường tiệm cận đứng.

Đáp án C