Một vật chuyển động theo quy luật (S = - {t^3} + 9{t^2} + t + 10 ), với (t ) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và (S ) (mét) là quảng đường vật đi được...

Câu hỏi :

Một vật chuyển động theo quy luật \(S = - {t^3} + 9{t^2} + t + 10\), với \(t\) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và \(S\) (mét) là quảng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 12 giây, kể từ lúc bắt đầu chuyển động tại thời điểm \(t\) bằng bao nhiêu giây thì vật đạt vận tốc lớn nhất?

* Đáp án

A

* Hướng dẫn giải

\(v\left( t \right) = S'\left( t \right) = - 3{t^2} + 18t + 1\) trên đoạn \(\left[ {0;12} \right].\)

Bảng biến thiên:

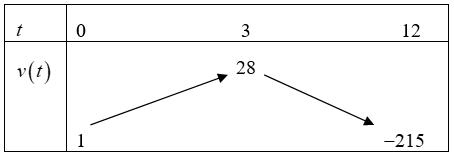
Vận tốc của chuyển động đạt giá trị lớn nhất theo dữ kiện của bài là: \(t = 3s.\)

Đáp án A