Cho hàm số (y = f left( x right) )có đồ thị của hàm số (f'(x) ) như sau:Trên khoảng (( - 10;10) ) có tất cả bao nhiêu số nguyên của để hàm số (g(x) = f(x) + mx + 2020 ) có đúng một...

* Hướng dẫn giải

Ta có: \(g'\left( x \right) = f'\left( x \right) + m\)

Cho \(g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = - m,\left( 1 \right)\)

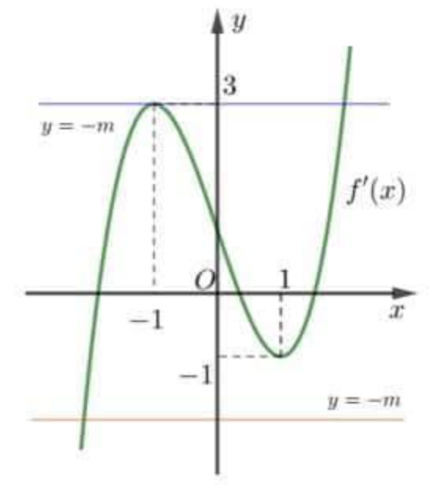
Hàm số \(g\left( x \right)\) có đúng một điểm cực trị khi và chỉ khi phương trình \(\left( 1 \right)\) có đúng một nghiệm bội lẻ \( \Leftrightarrow \left[ \begin{array}{l} - m \ge 3\\ - m \le - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \le - 3\\m \ge 1\end{array} \right..\)

Kết hợp điều kiện \(\left\{ \begin{array}{l}m \in \left( { - 10;10} \right)\\m \in \mathbb{Z}\end{array} \right. \Rightarrow m \in \left\{ { - 9, - 8, - 7, - 6, - 5, - 4, - 3,1,2,3,4,5,6,7,8,9} \right\}\)

Suy ra có 16 giá trị thỏa yêu cầu bài toán.\(m\)

Đáp án C