Có bao nhiêu giá trị nguyên âm của tham số (m ) để hàm số (y = {x^3} + mx - frac{1}{{5{x^2}}} ) đồng biến trên khoảng ( left( {0; + infty } right)? )

* Hướng dẫn giải

Ta có: \(y' = 3{x^2} + m + \frac{2}{{5{x^3}}}.\)

Hàm số \(y = {x^3} + mx - \frac{1}{{5{x^2}}}\) đồng biến trên \(\left( {0; + \infty } \right)\)

\( \Leftrightarrow y' \ge 0,\forall x \in \left( {0; + \infty } \right).\)

\( \Leftrightarrow 3{x^2} + m + \frac{2}{{5{x^3}}} \ge 0,\forall x \in \left( {0; + \infty } \right)\)

\( \Leftrightarrow m \ge - 3{x^2} - \frac{2}{{5{x^3}}},\forall x \in \left( {0; + \infty } \right)\)

\( \Leftrightarrow m \ge \mathop {\max }\limits_{\left( {0; + \infty } \right)} g\left( x \right)\) với \(g\left( x \right) = - 3{x^2} - \frac{2}{{5{x^3}}}.\)

Xét \(g\left( x \right) = - 3{x^2} - \frac{2}{{5{x^3}}}\) trên \(\left( {0; + \infty } \right),\) ta có \(g'\left( x \right) = - 6x + \frac{6}{{5{x^4}}};g'\left( x \right) = 0 \Leftrightarrow x = \frac{1}{{\sqrt[5]{5}}}.\)

Bảng biến thiên

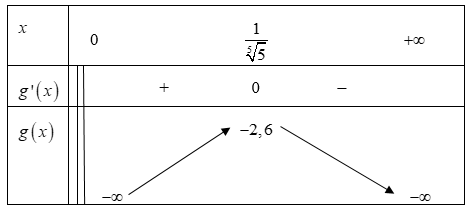
Từ bảng biến thiên suy ra \(m \ge - 2,6.\)

Vậy \(m = - 2\) và \(m = 1\) thỏa mãn.

Đáp án C