Cho tứ diện đều (ABCD ) cạnh (a. ) Lấy (N,M ) là trung điểm của (AB ) và (AC. ) Tính khoảng cách (d ) giữa (CN ) và (DM. )

* Hướng dẫn giải

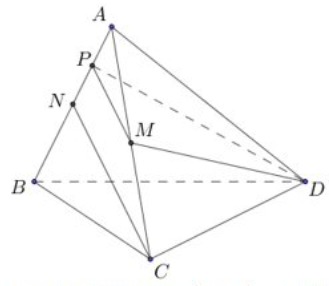
Gọi \(P\) là trung điểm của \(AN \Rightarrow MP//CN,MP \subset \left( {DMP} \right) \Rightarrow CN//\left( {DMP} \right)\)

\( \Rightarrow d\left( {CN,DM} \right) = d\left( {CN,\left( {DMP} \right)} \right) = d\left( {N,\left( {DMP} \right)} \right) = d\left( {A,\left( {DMP} \right)} \right).\)

Ta có \(ABCD\) là tứ diện đều cạnh \(a \Rightarrow {V_{ABCD}} = \frac{{{a^3}\sqrt 2 }}{{12}}.\)

Ta có \(\frac{{{V_{A.DMP}}}}{{{V_{A.DBC}}}} = \frac{{AP}}{{AB}}.\frac{{AM}}{{AC}} = \frac{1}{8} \Rightarrow {V_{A.DMP}} = \frac{1}{8}{V_{A.DBC}} = \frac{{{a^3}\sqrt 2 }}{{96}}.\)

Tam giác \(ACD\) đều cạnh \(a,\) có \(M\) là trung điểm của \(AC \Rightarrow DM = \frac{{a\sqrt 3 }}{2}.\)

Tam giác \(ABC\) đều cạnh \(a,\) có \(N\) là trung điểm của \(AB \Rightarrow CN = \frac{{a\sqrt 3 }}{2} \Rightarrow MP = \frac{1}{2}CN = \frac{{a\sqrt 3 }}{4}.\)

Tam giác \(ADP,\) có \(AP = \frac{a}{4},AD = a,\widehat {PAD} = {60^0}.\)

\( \Rightarrow DP = \sqrt {A{D^2} + A{P^2} - 2.AD.AP.\cos \widehat {PAD}} = \frac{{a\sqrt {13} }}{4}.\)

Đặt \(p = \frac{{DM + DP + MP}}{2} = \frac{{a\left( {\sqrt {13} + 3\sqrt 3 } \right)}}{8}.\)

\( \Rightarrow {S_{\Delta DMP}} = \sqrt {p\left( {p - DM} \right)\left( {p - DP} \right)\left( {p - MP} \right)} = \frac{{{a^2}\sqrt {35} }}{{32}}\)

Lại có \({V_{A.DMP}} = \frac{1}{3}{S_{\Delta DMP}}.d\left( {A,\left( {DMP} \right)} \right) \Rightarrow d\left( {A,\left( {DMP} \right)} \right) = \frac{{3{V_{A.DMP}}}}{{{V_{\Delta DMP}}}} = \frac{{3.\frac{{{a^3}\sqrt 2 }}{{96}}}}{{\frac{{{a^2}\sqrt {35} }}{{32}}}} = \frac{{a\sqrt {70} }}{{35}}.\)

Vậy \(d\left( {CN,DM} \right) = \frac{{a\sqrt {70} }}{{35}}.\)

Đáp án D