Cho lăng trụ tam giác đều (ABC.A'B'C' ) có cạnh đáy bằng (a. ) Trên các tia (AA',BB',CC' ) lần lượt lấy ({A_1},{B_1},{C_1} ) cách mặt phẳng đáy ( left( {ABC} right) ) một khoảng lầ...
Câu hỏi :
Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có cạnh đáy bằng \(a.\) Trên các tia \(AA',BB',CC'\) lần lượt lấy \({A_1},{B_1},{C_1}\) cách mặt phẳng đáy \(\left( {ABC} \right)\) một khoảng lần lượt là \(\frac{a}{2},a,\frac{{3a}}{2}.\) Tính góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {{A_1}{B_1}{C_1}} \right).\)
A.\({60^0}.\)
B. \({90^0}.\)
C.\({45^0}.\)
D.\({30^0}.\)
* Đáp án
C
* Hướng dẫn giải
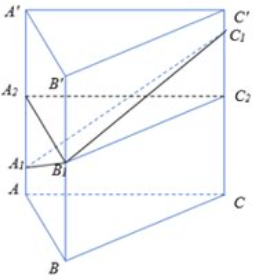
Từ \({B_1}\) dựng mặt phẳng song song với \(\left( {ABC} \right)\) cắt \(AA'\) và \(CC'\) tại \({A_2},{C_2}.\)
Ta có \({A_1}{A_2} = B{B_1} - A{A_1} = \frac{a}{2} \Rightarrow {A_1}{B_1} = \sqrt {{A_1}A_2^2 + {A_2}{B_1}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2},\) tương tự \({B_1}{C_1} = \frac{{a\sqrt 5 }}{2},{A_1}{C_1} = a\sqrt 2 .\) Vậy tam giác \({A_1}{B_1}{C_1}\) cân tại \({B_1}.\)
Khi đó đường cao ứng với đỉnh \({B_1}\) của tam giác \({A_1}{B_1}{C_1}\) là \(\sqrt {{B_1}C_1^2 - \frac{{{A_1}C_1^2}}{4}} = \frac{{a\sqrt 3 }}{2}\)
\({S_{\Delta {A_1}{B_1}{C_1}}} = \frac{{{a^2}\sqrt 6 }}{4};{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{4},\) mặt khác tam giác \(ABC\) là hình chiếu của tam giác \({A_1}{B_1}{C_1}\) trên mặt phẳng \(\left( {ABC} \right).\)
Gọi \(\varphi \) là góc giữa hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {{A_1}{B_1}{C_1}} \right).\)
Ta có \(\cos \varphi = \frac{{{S_{\Delta ABC}}}}{{{S_{{A_1}{B_1}{C_1}}}}} = \frac{{\sqrt 2 }}{2} \Rightarrow \varphi = {45^0}.\)
Đáp án C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Copyright © 2021 HOCTAP247
