Có bao nhiêu giá trị nguyên âm của (a ) để đồ thị hàm số (y = {x^3} + left( {a + 10} right){x^2} - x + 1 ) cắt trục hoành tại đúng một điểm?A. 10.

* Hướng dẫn giải

Xét phương trình hoành độ giao điểm \({x^3} + \left( {a + 10} \right){x^2} - x + 1 = 0{\rm{ }}\left( 1 \right) \Leftrightarrow {x^3} + 10{x^2} - x + 1 = - a{x^2}.\)

Nhận thấy \(x = 0\) không phải là nghiệm của phương trình nên

\({x^3} + \left( {a + 10} \right){x^2} - x + 1 = 0\left( 1 \right) \Leftrightarrow \frac{{{x^3} + 10{x^2} - x + 1}}{{ - {x^2}}} = a.\)

Xét hàm số \(f\left( x \right) = \frac{{{x^3} + 10{x^2} - x + 1}}{{ - {x^2}}} \Rightarrow f'\left( x \right) = \frac{{ - {x^3} - x + 2}}{{{x^3}}} = \frac{{ - \left( {{x^2} + x + 2} \right)\left( {x - 1} \right)}}{{{x^3}}}\)

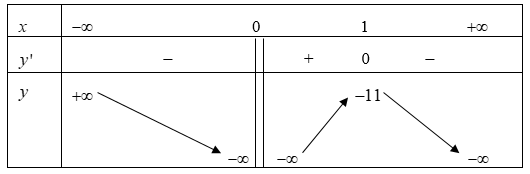
Từ bảng biến thiên ta thấy phương trình có một nghiệm khi \(a >- 11\) suy ra \(a \in \left\{ { - 10; - 9;...; - 1} \right\}.\)

Đáp án A